力扣刷题(二) #
力扣刷题 全部题目模块(101~200)
简单 #
对称二叉树 #
给你一个二叉树的根节点 root , 检查它是否轴对称。

输入:root = [1,2,2,3,4,4,3]
输出:true
//不能使用中序遍历后看其是否对称,例如[1,2,2,2,null,2]
func isSymmetric(root *TreeNode) bool {
return metric(root.Left,root.Right)
}
func metric(left *TreeNode,right *TreeNode) bool{
if left==nil&&right==nil{ //如果都为nil证明到底了返回true
return true
}
if left==nil||right==nil{ //一个为nil一个不为nil返回false
return false
}
if left.Val!=right.Val{ //不相等返回false
return false
}
return metric(left.Left,right.Right)&&metric(left.Right,right.Left) //将两边同时放进去递归
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.7 MB, 在所有 Go 提交中击败了67.20%的用户
相交链表 #
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
func getIntersectionNode(headA, headB *ListNode) *ListNode {
if headA==nil||headB==nil{ //假设无头结点
return nil
}
pa:=headA
pb:=headB
a,b:=1,1 //计数
for pa.Next!=nil{
pa=pa.Next
a++
}
for pb.Next!=nil{
pb=pb.Next
b++
}
if pa==pb{ //证明相交
if a>b{
n:=a-b
for i:=0;i<n;i++{
headA=headA.Next
}
for headA!=headB{
headA=headA.Next
headB=headB.Next
}
return headA
}else{
n:=b-a
for i:=0;i<n;i++{
headB=headB.Next
}
for headA!=headB{
headA=headA.Next
headB=headB.Next
}
return headA
}
}else{ //证明不相交
return nil
}
}
执行用时:16 ms, 在所有 Go 提交中击败了99.97%的用户
内存消耗:7 MB, 在所有 Go 提交中击败了72.22%的用户
二叉树等最大深度 #
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例: 给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
func maxDepth(root *TreeNode) int {
if root==nil{
return 0
}
Lefthight:=maxDepth(root.Left) //左子树高度
Righthight:=maxDepth(root.Right) //右子树高度
if Lefthight>Righthight{
return Lefthight+1
}
return Righthight+1
}
执行用时:4 ms, 在所有 Go 提交中击败了85.42%的用户
内存消耗:4 MB, 在所有 Go 提交中击败了79.88%的用户
func maxDepth(root *TreeNode) int { //层次遍历用法
if root==nil{
return 0
}
depath:=0 //深度
queue:=[]*TreeNode{} //定义队列
queue=append(queue,root) //根加入
for len(queue)>0{
queuelength:=len(queue) //记录队列长度
for i:=0;i<queuelength;i++{ //开始遍历,逐个取出,并加入子节点
c:=queue[0]
queue=queue[1:]
if c.Left!=nil{
queue=append(queue,c.Left)
}
if c.Right!=nil{
queue=append(queue,c.Right)
}
}
depath++ //一层结束 加一
}
return depath
}
执行用时:4 ms, 在所有 Go 提交中击败了85.42%的用户
内存消耗:4.1 MB, 在所有 Go 提交中击败了36.62%的用户
二叉树的最小深度 #
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。

输入:root = [3,9,20,null,null,15,7]
输出:2
func minDepth(root *TreeNode) int {
if root==nil{
return 0
}
Leftlength:=minDepth(root.Left)
Rightlength:=minDepth(root.Right)
if Leftlength>Rightlength{
if Rightlength==0{
return Leftlength+1
}
return Rightlength+1
}
if Leftlength<Rightlength{
if Leftlength==0{
return Rightlength+1
}
}
return Leftlength+1
}
3 //排除一方都为nil的情况
\
20
\
7
执行用时:164 ms, 在所有 Go 提交中击败了58.93%的用户
内存消耗:18.8 MB, 在所有 Go 提交中击败了45.34%的用户
func minDepth(root *TreeNode) int {
if root==nil{
return 0
}
depth:=0
queue:=list.New() //创建队列 New
queue.PushBack(root)
for queue.Len()>0{ //长度 Len()记住
queuelength:=queue.Len()
for i:=0;i<queuelength;i++{
cc:=queue.Remove(queue.Front()).(*TreeNode) //记住queue.Remove(queue.Front())
if cc.Left==nil&&cc.Right==nil{ //两个都为nil证明到了最低点 直接返回
return depth+1
}
if cc.Left!=nil{
queue.PushBack(cc.Left)
}
if cc.Right!=nil{
queue.PushBack(cc.Right)
}
}
depth++
}
return depth
}
执行用时:148 ms, 在所有 Go 提交中击败了98.31%的用户
内存消耗:18.8 MB, 在所有 Go 提交中击败了47.27%的用户
将有序数组转换为二叉搜索树 #
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

func sortedArrayToBST(nums []int) *TreeNode { //递归思想,往下构造
if len(nums)==0{ //如果nums为空,返回nil
return nil
}
mid:=(len(nums)-1)/2
root:=&TreeNode{
Val:nums[mid],
Left:sortedArrayToBST(nums[:mid]),
Right:sortedArrayToBST(nums[mid+1:])}
return root
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:3.3 MB, 在所有 Go 提交中击败了48.72%的用户
平衡二叉树 #
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

输入:root = [3,9,20,null,null,15,7]
输出:true
func isBalanced(root *TreeNode) bool {
c:=balance(root)
if c==-1{
return false
}
return true
}
func balance(root *TreeNode)(hight int){ //返回高度
if root==nil{
return 0
}
lefthight:=balance(root.Left)
righthight:=balance(root.Right)
if lefthight==-1||righthight==-1{ //返回条件,如果一个证明不是平衡 则返回-1
return -1
}
if abc(lefthight,righthight)==-1{ //判断两边相减 是否>1或则<-1
return -1
}
return max(lefthight,righthight)+1 //不是的的话,返回最大值并加上本层数量 +1
}
func abc(lefthight int,righthight int)(c int){
a:=lefthight-righthight
if a<0{
a=-a
}
if a>1{
return -1
}
return a
}
func max(lefthight int,righthight int)(c int){
if lefthight>righthight{
return lefthight
}else{
return righthight
}
return lefthight
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:5.5 MB, 在所有 Go 提交中击败了65.96%的用户
路径总和 #
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。

输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
func hasPathSum(root *TreeNode, targetSum int) bool {
if root==nil{
return false
}
if root.Left==nil&&root.Right==nil{
return targetSum-root.Val==0
}
return hasPathSum(root.Left,targetSum-root.Val)||hasPathSum(root.Right,targetSum-root.Val)
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:4.4 MB, 在所有 Go 提交中击败了99.72%的用户
杨辉三角 #
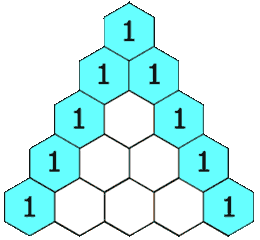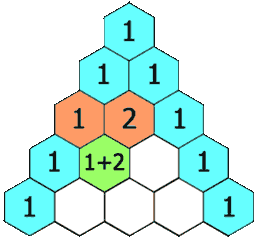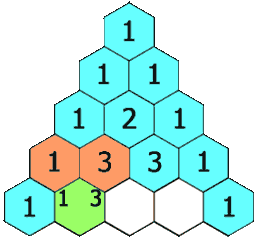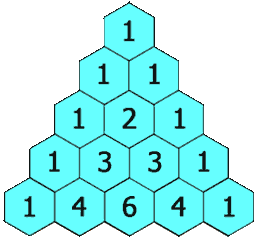
给定一个非负整数 *numRows,*生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
func generate(numRows int) [][]int {
marry:=[][]int{}
if numRows==1{ //等于1 则返回1
marry=append(marry,[]int{1})
return marry
}
arry:=[]int{1}
marry=append(marry,arry)
for i:=2;i<=numRows;i++{ //从二开始逐渐往里面加
arrylength:=len(arry)
cc:=[]int{}
for j:=0;j<=arrylength;j++{ //总共加arrylength+1次
if j==0||j==arrylength{ //头和尾加1
cc=append(cc,1)
}else{ //不是头和尾
cc=append(cc,arry[j-1]+arry[j]) //上一个加本位
}
}
marry=append(marry,cc) //插入
arry=cc //改变arry的值
}
return marry
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:1.9 MB, 在所有 Go 提交中击败了87.70%的用户
func generate(numRows int) [][]int {
ans := make([][]int, numRows)
for i := range ans {
ans[i] = make([]int, i+1)
ans[i][0] = 1
ans[i][i] = 1
for j := 1; j < i; j++ {
ans[i][j] = ans[i-1][j] + ans[i-1][j-1]
}
}
return ans
}
杨辉三角2 #
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

输入: rowIndex = 3
输出: [1,3,3,1]
func getRow(rowIndex int) []int { // 2
marry:=make([]int,rowIndex+1) //长度加一 1 0 0
marry[0]=1 // 1 0 0
for i:=1;i<=rowIndex;i++{ // 从第二层开始循环 1 1 0
for j:=i;j>0;j--{ // 与前面相加 因为最后一个是0 1 2 1
marry[j]=marry[j]+marry[j-1]
}
}
return marry
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:1.8 MB, 在所有 Go 提交中击败了99.86%的用户
买卖股票的最佳时机 #
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
func maxProfit(prices []int) int {
length:=len(prices)
if length==1{
return 0
}
min,max:=prices[0],0 //定义最大值和最小值
for i:=1;i<length;i++{ //一定要一次for循环,否则超时
max=Max(max,prices[i]-min) //找出这个值减去最小值后,跟最大值那个大
min=Min(min,prices[i]) //找出最小值
}
return max
}
func Max(x,y int)int{
if x>y{
return x
}
return y
}
func Min(x,y int)int{
if x>y{
return y
}
return x
}
执行用时:100 ms, 在所有 Go 提交中击败了74.55%的用户
内存消耗:7.8 MB, 在所有 Go 提交中击败了41.89%的用户
验证回文串 #
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。
字母和数字都属于字母数字字符。
给你一个字符串 s,如果它是 回文串 ,返回 true ;否则,返回 false 。
输入: s = "A man, a plan, a canal: Panama"
输出:true
解释:"amanaplanacanalpanama" 是回文串。
func isPalindrome(s string) bool {
var ss string
for i:=0;i<len(s);i++{
if isalnum(s[i]){ //是那几个
ss=ss+string(s[i]) //拼接,不是就跳过
}
}
ss=strings.ToLower(ss) //将字符串变为小写 大写是string.ToUpper(ss)
for i,j:=0,len(ss)-1;i<j;i++{ //判断是否回文
if ss[i]!=ss[j]{
return false
}
j--
}
return true
}
func isalnum(ch byte)bool{ //如果是这几个范围内 返回true
return (ch>='A'&&ch<='Z')||(ch>='a'&&ch<='z')||(ch>='0'&&ch<='9')
}
执行用时:180 ms, 在所有 Go 提交中击败了18.85%的用户
内存消耗:8.6 MB, 在所有 Go 提交中击败了16.28%的用户
只出现一次的数字 #
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
输入: [2,2,1]
输出: 1
func singleNumber(nums []int) int {
sort.Ints(nums) //先排序
for i:=0;i<len(nums)-1;i++{
if nums[i]!=nums[i+1]{
if i==0{ //排除为第一个
return nums[i]
}
if i==len(nums)-2{ //排除为最后一个
return nums[i+1]
}
if nums[i]!=nums[i-1]{ //前后都不一样 正确答案
return nums[i]
}
}
}
return nums[0]
}
执行用时:32 ms, 在所有 Go 提交中击败了5.33%的用户
内存消耗:6 MB, 在所有 Go 提交中击败了24.70%的用户
环形链表 #
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。

输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
func hasCycle(head *ListNode) bool {
if head==nil||head.Next==nil{
return false
}
fast:=head
low:=head
for fast!=nil&&fast.Next!=nil {
fast=fast.Next.Next
low=low.Next
if fast==low{
return true
}
}
return false
}
执行用时:8 ms, 在所有 Go 提交中击败了48.05%的用户
内存消耗:4.2 MB, 在所有 Go 提交中击败了99.98%的用户
二叉树的前序遍历 #
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
输入:root = [1,null,2,3]
输出:[1,2,3]
func preorderTraversal(root *TreeNode) []int {
nums:=[]int{}
var dfs func(root *TreeNode)
dfs=func (root *TreeNode){
if root==nil{
return
}
nums=append(nums,root.Val)
dfs(root.Left)
dfs(root.Right)
}
dfs(root)
return nums
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:1.9 MB, 在所有 Go 提交中击败了99.77%的用户
二叉树的后序遍历 #
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
输入:root = [1,null,2,3]
输出:[3,2,1]
func postorderTraversal(root *TreeNode) []int {
nums:=[]int{}
var dfs func(root *TreeNode)
dfs=func (root *TreeNode){
if root==nil{
return
}
dfs(root.Left)
dfs(root.Right)
nums=append(nums,root.Val)
}
dfs(root)
return nums
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:1.9 MB, 在所有 Go 提交中击败了99.75%的用户
中等 #
二叉树的层序遍历 #
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
func levelOrder(root *TreeNode) [][]int { //递归
marry:=[][]int{}
depath:=0 //层数
var order func(root *TreeNode,depath int)
order=func(root *TreeNode,depath int){
if root==nil{ //不返回下面会报错
return
}
if len(marry)==depath{ //长度等于depath 就新建一个,往里面填数据
marry=append(marry,[]int{})
}
marry[depath]=append(marry[depath],root.Val) //很巧妙
order(root.Left,depath+1)
order(root.Right,depath+1)
}
order(root,depath)
return marry
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.9 MB, 在所有 Go 提交中击败了7.78%的用户
func levelOrder(root *TreeNode) [][]int {
marry:=[][]int{}
if root==nil{
return marry
}
queue:=list.New() //创建一个队列
queue.PushBack(root) //root入队
arry:=[]int{}
for queue.Len()>0{
queuelength:=queue.Len() //保存当前层的长度,然后处理当前层
for i:=0;i<queuelength;i++{
node:=queue.Remove(queue.Front()).(*TreeNode) //出队列 .(*TreeNode)出来为指针
if node.Left!=nil{
queue.PushBack(node.Left)
}
if node.Right!=nil{
queue.PushBack(node.Right)
}
arry=append(arry,node.Val) //将值加入本层切片中
}
marry=append(marry,arry) //放入结果集
arry=[]int{} //清空层的数据 很重要
}
return marry
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.8 MB, 在所有 Go 提交中击败了19.56%的用户
二叉树等锯齿形层序遍历 #
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
func zigzagLevelOrder(root *TreeNode) [][]int {
marry:=[][]int{}
if root==nil{
return marry
}
queue:=[]*TreeNode{root} //创建一个队列 // 当前层
arry:=[]int{}
x:=true // 初始方向
for len(queue)>0{
queuelength:=len(queue)
queue2:= []*TreeNode{} // 构造下一层
for i:=0;i<queuelength;i++{
if x==true{
arry=append(arry,queue[i].Val)
}else{
arry=append([]int{queue[i].Val},arry...)// 添加元素到头部
}
if queue[i].Left!=nil{
queue2=append(queue2,queue[i].Left)
}
if queue[i].Right!=nil{
queue2=append(queue2,queue[i].Right)
}
}
marry=append(marry,arry)
arry=[]int{} //清空
x=!x //改变方向
queue=queue2 // 更新当前层
}
return marry
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.8 MB, 在所有 Go 提交中击败了9.26%的用户
func zigzagLevelOrder(root *TreeNode) [][]int { //错误答案
marry:=[][]int{}
if root==nil{
return marry
}
queue:=list.New() //创建一个队列
queue.PushBack(root) //root入队
x:=true
for queue.Len()>0{
queuelength:=queue.Len()
arry:=[]int{}
for i:=0;i<queuelength;i++{
node:=queue.Remove(queue.Front()).(*TreeNode) //列表为双向循环链表,你不能这样用
if x==true{
if root.Left!=nil{
queue.PushFront(root.Left)
}
if root.Right!=nil{
queue.PushFront(root.Right)
}
}else{
if root.Left!=nil{
queue.PushBack(root.Left)
}
if root.Right!=nil{
queue.PushBack(root.Right)
}
}
arry=append(arry,node.Val)
}
marry=append(marry,arry)
x=!x
}
return marry
}
从前序与中序遍历序列构造二叉树 #
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
func buildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder)==0||len(inorder)==0{
return nil
}
//取前序遍历的第一个元素为根节点值
rootvalue:=preorder[0]
//在中序遍历中找到该值下标,左边为左子树,右边为右子树
left:=findRoot(inorder,rootvalue)
//构造树
root:=&TreeNode{
Val:rootvalue,
Left:buildTree(preorder[1:left+1],inorder[:left]),
Right:buildTree(preorder[left+1:],inorder[left+1:])}
return root
}
func findRoot(inorder []int,rootvalue int)(left int){
for i:=0;i<len(inorder);i++{
if rootvalue==inorder[i]{
return i
}
}
return -1
}
执行用时:4 ms, 在所有 Go 提交中击败了92.79%的用户
内存消耗:4 MB, 在所有 Go 提交中击败了82.47%的用户
从中序后序遍历序列构造二叉树 #
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。

提示:
* 1 <= inorder.length <= 3000
* postorder.length == inorder.length
* -3000 <= inorder[i], postorder[i] <= 3000
* inorder 和 postorder 都由 不同 的值组成
* postorder 中每一个值都在 inorder 中
* inorder 保证是树的中序遍历
* postorder 保证是树的后序遍历
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来在切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
如果让我们肉眼看两个序列,画一棵二叉树的话,应该分分钟都可以画出来。
流程如图:

说到一层一层切割,就应该想到了递归。
来看一下一共分几步:
- 第一步:如果数组大小为零的话,说明是空节点了。
- 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
- 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
- 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
- 第五步:切割后序数组,切成后序左数组和后序右数组
- 第六步:递归处理左区间和右区间
func buildTree(inorder []int, postorder []int) *TreeNode {
if len(postorder)==0||len(inorder)==0{//如果前序数组或后序数组为0,返回
return nil
}
//第二步,拿到后序遍历数组的最后一个元素,就是当前的中间节点的值
rootvalue:=postorder[len(postorder)-1]
//从中序遍历中找到一分为二的点,左边为左子树,右边为右子树 下标
left:=findRootIndex(inorder,rootvalue)
//构造树
root:=&TreeNode{
Val:rootvalue,
Left:buildTree(inorder[:left],postorder[:left]),//将后序遍历一分为二,左边为左子树,右边为右子树
Right:buildTree(inorder[left+1:],postorder[left:len(postorder)-1]) //最后根节点去掉
}
return root
}
func findRootIndex(inorder []int,rootvalue int) (left int){
for i:=0;i<len(inorder);i++{
if rootvalue==inorder[i]{
return i
}
}
return -1
}
执行用时:4 ms, 在所有 Go 提交中击败了88.89%的用户
内存消耗:4 MB, 在所有 Go 提交中击败了58.31%的用户
二叉树的层序遍历2 #
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)

输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
func levelOrderBottom(root *TreeNode) [][]int {
marry:=[][]int{}
if root==nil{
return marry
}
queue:=list.New()
queue.PushBack(root)
for queue.Len()>0{
length:=queue.Len()
arry:=[]int{}
for i:=0;i<length;i++{
root:=queue.Remove(queue.Front()).(*TreeNode)
if root.Left!=nil{
queue.PushBack(root.Left)
}
if root.Right!=nil{
queue.PushBack(root.Right)
}
arry=append(arry,root.Val)
}
marry=append(marry,arry)
}
maay:=[][]int{}
for i:=len(marry)-1;i>-1;i--{
maay=append(maay,marry[i])
}
return maay
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.9 MB, 在所有 Go 提交中击败了20.82%的用户
有序链表转换为二叉搜索树 #
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1

输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
//也是递归,先找中间节点,链表中间节点用快慢指针法
func sortedListToBST(head *ListNode) *TreeNode {
root:=sortTree(head,nil)
return root
}
func midnode(left,right *ListNode)*ListNode{ //找到中间节点指针
fast,slow:=left,left
for fast!=right&&fast.Next!=right{
fast=fast.Next.Next
slow=slow.Next
}
return slow
}
func sortTree(left,right *ListNode)*TreeNode{
if left==right{ //左 ==右 则搞完了 返回
return nil
}
mid:=midnode(left,right) //找中间节点
root:=&TreeNode{
Val:mid.Val,
Left:sortTree(left,mid), //递归调用
Right:sortTree(mid.Next,right)}
return root
}
执行用时:8 ms, 在所有 Go 提交中击败了20.75%的用户
内存消耗:5.6 MB, 在所有 Go 提交中击败了100.00%的用户
路径总和2 #
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
var marry [][]int
func pathSum(root *TreeNode, targetSum int) [][]int { //回溯法
marry=[][]int{}
if root==nil{
return marry
}
tmp:=[]int{}
target(root,targetSum,0,tmp)
return marry
}
func target(root *TreeNode,targetSum int,sum int,tmp []int){
sum=sum+root.Val
tmp=append(tmp,root.Val) //在函数里面做的操作,回溯时不需要回退
if targetSum==sum&&root.Left==nil&&root.Right==nil{ //相等,且为叶子节点
cc:=make([]int,len(tmp))
copy(cc,tmp)
marry=append(marry,cc)
}
if root.Left!=nil{
target(root.Left,targetSum,sum,tmp)
}
if root.Right!=nil{
target(root.Right,targetSum,sum,tmp) //不需要回退,在进入函数之前如果操作了需要回退
}
}
执行用时:4 ms, 在所有 Go 提交中击败了85.02%的用户
内存消耗:4.3 MB, 在所有 Go 提交中击败了80.78%的用户
二叉树展开为链表 #
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。 展开后的单链表应该与二叉树 先序遍历 顺序相同。

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
1
/ \
2 5
/ \ \
3 4 6
//将 1 的左子树插入到右子树的地方
1
\
2 5
/ \ \
3 4 6
//将原来的右子树接到左子树的最右边节点
1
\
2
/ \
3 4
\
5
\
6
//将 2 的左子树插入到右子树的地方
1
\
2
\
3 4
\
5
\
6
//将原来的右子树接到左子树的最右边节点
1
\
2
\
3
\
4
\
5
\
6
......
func flatten(root *TreeNode) {
curr:=root
for curr!=nil{
if curr.Left==nil{
if curr.Right==nil{
return
}else{
curr=curr.Right //进入下一轮
}
}else{
leftrigh:=curr.Left
for leftrigh.Right!=nil{ //寻找左子树最右边
leftrigh=leftrigh.Right
}
leftrigh.Right=curr.Right //拼接
curr.Right=curr.Left
curr.Left=nil
curr=curr.Right //进入下一轮
}
}
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.8 MB, 在所有 Go 提交中击败了69.10%的用户
填充每个节点的下一个右侧节点指针 #
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。

输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
func connect(root *Node) *Node { //一层一层去搞想起来层序遍历
if root==nil{
return nil
}
arry:=[]*Node{}
arry=append(arry,root)
for len(arry)>0{ //长度大于0时继续
x:=len(arry) //把这个值定死,遍历,存值
for i:=0;i<x;i++{
node:=arry[0]
arry=arry[1:] //拿一个 去掉一个 出队列
if x-i>1{ //精髓在于x-i>1,因为后面在不断的加入,不能用len(arry)>0
node.Next=arry[0] //让他指向同层下一个
}else{
node.Next=nil //到末尾了 赋nil
}
if node.Left!=nil{ //逐个加入数组
arry=append(arry,node.Left)
}
if node.Right!=nil{
arry=append(arry,node.Right)
}
}
}
return root
}
执行用时:4 ms, 在所有 Go 提交中击败了91.30%的用户
内存消耗:6.5 MB, 在所有 Go 提交中击败了19.79%的用户
填充每个节点的下一个右侧节点指针2 #
给定一个二叉树
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。初始状态下,所有 next 指针都被设置为 NULL。
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。

输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
func connect(root *Node) *Node { //补充节点的右侧指针,不是完美二叉树
if root==nil||(root.Left==nil&&root.Right==nil){
return root
}
if root.Left!=nil&&root.Right!=nil{ //左右子树都在,左指向右,右去给他找
root.Left.Next=root.Right
root.Right.Next=conn(root)
}
if root.Left==nil{ //左边为空,右去给他找
root.Right.Next=conn(root)
}
if root.Right==nil{ //右边为空,左去给他找
root.Left.Next=conn(root)
}
//这里要注意:先递归右子树,否则右子树根节点next关系没建立好,左子树到右子树子节点无法正确挂载
root.Right=connect(root.Right)
root.Left=connect(root.Left)
return root
}
func conn(root *Node)*Node{ //一路向右找到有子节点的根节点
for root.Next!=nil{ //寻找的是root子树的Next,故在root.Next的子树中找
if root.Next.Left!=nil{ //左子树存在,则返回左子树
return root.Next.Left
}
if root.Next.Right!=nil{ //左子树不在,右子树在,返回右子树
return root.Next.Right
}
root=root.Next //都不在,在root.next.next中的左右子树找
}
return nil //如果root.Next为空,则直接返回nil,证明到最后面了
}
执行用时:4 ms, 在所有 Go 提交中击败了70.02%的用户
内存消耗:6 MB, 在所有 Go 提交中击败了99.25%的用户
三角形最小路径和 #
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
func minimumTotal(triangle [][]int) int {
x:=len(triangle)
for i:=1;i<x;i++{
for j:=0;j<len(triangle[i]);j++{
if j==0{ //如果是第一列,让这个值等于上一个 加这个值之和
triangle[i][j]=triangle[i][j]+triangle[i-1][j]
}
if j==len(triangle[i-1]){ //如果是最后一列,左上角加的东西
triangle[i][j]=triangle[i][j]+triangle[i-1][j-1]
}
if j>0&&j<len(triangle[i-1]){ //如果是中间的
lift:=triangle[i][j]+triangle[i-1][j]
right:=triangle[i][j]+triangle[i-1][j-1]
if lift>right{ //判断那个最小 让他等于那个
triangle[i][j]=right
}else{
triangle[i][j]=lift
}
}
}
}
y:=triangle[x-1][0]
for i:=1;i<len(triangle[x-1]);i++{ //在最后一列里面找最小的
if y<triangle[x-1][i]{
continue
}else{
y=triangle[x-1][i]
}
}
return y
}
执行用时:4 ms, 在所有 Go 提交中击败了92.81%的用户
内存消耗:3.1 MB, 在所有 Go 提交中击败了100.00%的用户
买卖股票的最佳时机2 #
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
func maxProfit(prices []int) int { //只要今天比昨天大,就卖出。 看了一眼评论,真大神
length:=len(prices)
ans:=0
for i:=1;i<length;i++{
if prices[i]>prices[i-1]{
ans=ans+prices[i]-prices[i-1]
}
}
return ans
}
执行用时:4 ms, 在所有 Go 提交中击败了88.93%的用户
内存消耗:2.9 MB, 在所有 Go 提交中击败了70.31%的用户
最长连续序列 #
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
func longestConsecutive(nums []int) int {//凡是要求时间复杂度的,以空间换时间
numap:=map[int]bool{}
for _,i:=range nums{ //以nums值为键创建map
numap[i]=true
}
longestStreak:=0 //返回最大区间
for num:=range numap{ //遍历map,num=键
if !numap[num-1]{ //如果numap[num-1]==false 意思就是没查到 如果能查到,证明不是最小的那个
currentNum:=num
currentStreak:=1 //从连续最小的进来
for numap[currentNum+1]{ //逐个往上查,查到就++
currentNum++
currentStreak++
}
if longestStreak<currentStreak{ //修改最大值
longestStreak=currentStreak
}
}
}
return longestStreak
}
执行用时:64 ms, 在所有 Go 提交中击败了70.63%的用户
内存消耗:9.5 MB, 在所有 Go 提交中击败了53.29%的用户
求根节点到叶节点数字之和 #
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。 计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。

输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
func sumNumbers(root *TreeNode) int {
cc:=sumNode(root,0)
return cc
}
func sumNode(root *TreeNode,sum int)int{ //记录总数
if root==nil{
return 0
}
sum=sum*10+root.Val //sum=上面的*10加本值
if root.Left==nil&&root.Right==nil{ //证明到底了
return sum
}
return sumNode(root.Left,sum)+sumNode(root.Right,sum) //左右和
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2 MB, 在所有 Go 提交中击败了31.73%的用户
被围绕到区域 #
给你一个 m x n 的矩阵 board ,由若干字符 ‘X’ 和 ‘O’ ,找到所有被 ‘X’ 围绕的区域,并将这些区域里所有的 ‘O’ 用 ‘X’ 填充。

输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
var m,n int
func solve(board [][]byte) {
m,n=len(board),len(board[0])
if m==0||n==0{
return
}
for i:=0;i<m;i++{ //把边缘输进去,递归
for j:=0;j<n;j++{
if i==0||i==m-1{ //第一行和最后一行
dfs(board,i,j)
}else{
if j==0||j==n-1{ //第一列和最后一列
dfs(board,i,j)
}
}
}
}
for i:=0;i<m;i++{
for j:=0;j<n;j++{
if board[i][j]=='O'{ //如果遇到O,变为X,如果遇到A变为O
board[i][j]='X'
}else if board[i][j]=='A'{
board[i][j]='O'
}
}
}
}
func dfs(board [][]byte, x int,y int){ //创造递归函数
if x<0||x>m-1||y<0||y>n-1||board[x][y]!='O'{ //超出的返回,如果是X也返回,从外面排除把O-A
return
}
board[x][y]='A'
dfs(board,x+1,y) //上下左右分别探查
dfs(board,x-1,y)
dfs(board,x,y+1)
dfs(board,x,y-1)
}
执行用时:32 ms, 在所有 Go 提交中击败了7.70%的用户
内存消耗:6.1 MB, 在所有 Go 提交中击败了84.59%的用户
分割回文串 #
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
func partition(s string) [][]string { //还是太笨了 指针没看懂
var marry [][]string //结果集合
var tmp []string //切割字符串集合
backtarceing(s, tmp, 0, &marry)
return marry
}
func backtarceing(s string, tmp []string, start int, marry *[][]string) {//不想用指针就别把他传进来,设置全局变量
if start == len(s) { //到达字符串的末尾了
ccc := make([]string, len(tmp))
copy(ccc, tmp)
*marry = append(*marry, ccc)
}
for i := start; i < len(s); i++ {
//处理(首先通过start和i判断切割的区间,进而判断该区间的字符串是否为回文,若为回文,则加入到tmp,否则继续后移,找到回文区间)(这里为一层处理)
if isPalindrome(s, start, i) {
tmp = append(tmp, s[start:i+1])
} else {
continue
}
backtarceing(s, tmp, i+1, marry) //递归 这里不传指针,退出来的时候marry==nil
tmp = tmp[:len(tmp)-1]
}
}
func isPalindrome(s string, start, end int) bool { //判断是否回文
for start < end {
if s[start] != s[end] {
return false
}
start++
end--
}
return true
}
执行用时:236 ms, 在所有 Go 提交中击败了64.42%的用户
内存消耗:24.2 MB, 在所有 Go 提交中击败了56.10%的用户
克隆图 #
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List<Node> neighbors;
}
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

func cloneGraph(node *Node) *Node { //深度优先遍历
visited := map[*Node]*Node{}
var cg func(node *Node) *Node
cg = func(node *Node) *Node {
if node == nil {
return node
}
// 如果该节点已经被访问过了,则直接从哈希表中取出对应的克隆节点返回
if _, ok := visited[node]; ok {
return visited[node]
}
// 克隆节点,注意到为了深拷贝我们不会克隆它的邻居的列表
cloneNode := &Node{node.Val, []*Node{}}
// 哈希表存储
visited[node] = cloneNode
// 遍历该节点的邻居并更新克隆节点的邻居列表
for _, n := range node.Neighbors {
cloneNode.Neighbors = append(cloneNode.Neighbors, cg(n))
}
return cloneNode
}
return cg(node)
}
func cloneGraph(node *Node) *Node { //广度优先遍历
if node == nil {
return node
}
visited := map[*Node]*Node{}
// 将题目给定的节点添加到队列
queue := []*Node{node}
// 克隆第一个节点并存储到哈希表中
visited[node] = &Node{node.Val, []*Node{}}
// 广度优先搜索
for len(queue) > 0 {
// 取出队列的头节点
n := queue[0]
// 遍历该节点的邻居
queue = queue[1:]
for _, neighbor := range n.Neighbors {
if _, ok := visited[neighbor]; !ok {
// 如果没有被访问过,就克隆并存储在哈希表中
visited[neighbor] = &Node{neighbor.Val, []*Node{}}
// 将邻居节点加入队列中
queue = append(queue, neighbor)
}
// 更新当前节点的邻居列表
visited[n].Neighbors = append(visited[n].Neighbors, visited[neighbor])
}
}
return visited[node]
}
环型链表2 #
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。

输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
//当发现slow与fast相遇时,我们再额外使用一个指针ptr。起始,它指向链表头部;随后,它和slow每次向后移动一个位置。最终,它们会在入环点相遇。
func detectCycle(head *ListNode) *ListNode {
if head==nil||head.Next==nil{
return nil
}
fast:=head
low:=head
for fast!=nil&&fast.Next!=nil{
fast=fast.Next.Next
low=low.Next
if fast==low{
pre:=head
for pre!=low{
pre=pre.Next
low=low.Next
}
return low
}
}
return nil
}
执行用时:4 ms, 在所有 Go 提交中击败了94.56%的用户
内存消耗:3.5 MB, 在所有 Go 提交中击败了77.44%的用户
LRU缓存 #
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存 int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。 void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。 函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
type LRUCache struct {
size int
capacity int
cache map[int]*DLinkedNode
head, tail *DLinkedNode
}
type DLinkedNode struct {
key, value int
prev, next *DLinkedNode
}
func initDLinkedNode(key, value int) *DLinkedNode {
return &DLinkedNode{
key: key,
value: value,
}
}
func Constructor(capacity int) LRUCache {
l := LRUCache{
cache: map[int]*DLinkedNode{},
head: initDLinkedNode(0, 0),
tail: initDLinkedNode(0, 0),
capacity: capacity,
}
l.head.next = l.tail
l.tail.prev = l.head
return l
}
func (this *LRUCache) Get(key int) int {
if _, ok := this.cache[key]; !ok {
return -1
}
node := this.cache[key]
this.moveToHead(node)
return node.value
}
func (this *LRUCache) Put(key int, value int) {
if _, ok := this.cache[key]; !ok {
node := initDLinkedNode(key, value)
this.cache[key] = node
this.addToHead(node)
this.size++
if this.size > this.capacity {
removed := this.removeTail()
delete(this.cache, removed.key)
this.size--
}
} else {
node := this.cache[key]
node.value = value
this.moveToHead(node)
}
}
func (this *LRUCache) addToHead(node *DLinkedNode) {
node.prev = this.head
node.next = this.head.next
this.head.next.prev = node
this.head.next = node
}
func (this *LRUCache) removeNode(node *DLinkedNode) {
node.prev.next = node.next
node.next.prev = node.prev
}
func (this *LRUCache) moveToHead(node *DLinkedNode) {
this.removeNode(node)
this.addToHead(node)
}
func (this *LRUCache) removeTail() *DLinkedNode {
node := this.tail.prev
this.removeNode(node)
return node
}
寻找峰值 #
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
func findPeakElement( nums []int ) int { //跟上面很像
left,right:=0,len(nums)-1
i:=0
for left<right{
i=left+(right-left)/2 //中间值
if i-1>-1&&i+1<len(nums){ //判断不在两边的情况
if nums[i]>nums[i+1]&&nums[i]>nums[i-1]{
return i
}
if nums[i]<nums[i+1]{
left=i+1
}else{
right=i-1
}
}
if i-1==-1{ //如果在最左边
if nums[i]>nums[i+1]{
return i
}
left=i+1 //这里++可能退出循环,left==right
}
if i+1==len(nums){ //如果在最右边
if nums[i]>nums[i-1]{
return i
}
right=i-1 //这里--可能退出循环,left==right
}
}
return left //所以要输入left的值
}
func findPeakElement(nums []int) int { //利用二分法
n := len(nums)
// 辅助函数,输入下标 i,返回 nums[i] 的值
// 方便处理 nums[-1] 以及 nums[n] 的边界情况
get := func(i int) int { //判断函数,如果是-1或者n,输出最小的值
if i == -1 || i == n {
return math.MinInt64
}
return nums[i]
}
left, right := 0, n-1
for {
mid := left+(right-left) / 2
if get(mid-1) < get(mid) && get(mid) > get(mid+1) { //如果是则输出
return mid
}
if get(mid) < get(mid+1) { //不是则改变left和right的值
left = mid + 1
} else {
right = mid - 1
}
}
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.6 MB, 在所有 Go 提交中击败了100.00%的用户
比较版本号 #
给你两个版本号 version1 和 version2 ,请你比较它们。
版本号由一个或多个修订号组成,各修订号由一个 ‘.’ 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。
比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。
返回规则如下:
如果 version1 > version2 返回 1,
如果 version1 < version2 返回 -1,
除此之外返回 0。
输入:version1 = "1.01", version2 = "1.001"
输出:0
解释:忽略前导零,"01" 和 "001" 都表示相同的整数 "1"
func compare( version1 string , version2 string ) int {
n1,n2:=len(version1),len(version2)
i,j:=0,0
for i<n1||j<n2{ //双指针
x:=0
for ;i<n1&&version1[i]!='.';i++{ //i<n1,且没有到.的时候
x=x*10+int(version1[i]-'0')
}
i++ //跳过.号
y:=0
for ;j<n2&&version2[j]!='.';j++{
y=y*10+int(version2[j]-'0')
}
j++ //跳过.号
if x>y{
return 1
}
if x<y{
return -1
}
}
return 0 //相等
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:1.8 MB, 在所有 Go 提交中击败了82.02%的用户
二叉树的右视图 #
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。

func rightSideView(root *TreeNode) []int { //层序遍历
root:=treeNode(xianxu,zhongxu)
arry:=[]int{}
if root==nil{ //开始层序遍历
return arry
}
queue:=[]*TreeNode{}
queue=append(queue,root)
for len(queue)>0{ //注意这里条件
length:=len(queue)
arry=append(arry,queue[length-1].Val) //输出最右边的
for j:=0;j<length;j++{
if queue[j].Left!=nil{
queue=append(queue,queue[j].Left)
}
if queue[j].Right!=nil{
queue=append(queue,queue[j].Right)
}
}
queue=queue[length:]
}
return arry
}
执行用时:0 ms, 在所有 Go 提交中击败了100.00%的用户
内存消耗:2.1 MB, 在所有 Go 提交中击败了42.83%的用户
岛屿数量 #
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
func solve( grid [][]byte ) int {
n:=0
a:=len(grid)
b:=len(grid[0])
var backtrace func(i int,j int) //递归函数
backtrace=func(i, j int) {
grid[i][j]='0' //先把到的地方变为‘0’
if i>=0&&i+1<a&&grid[i+1][j]=='1'{ //如果它[i+1][j]=='1'继续递归 变为0
backtrace(i+1,j)
}
if i-1>=0&&i<a&&grid[i-1][j]=='1'{ //如果它[i-1][j]=='1'继续递归 变为0
backtrace(i-1,j)
}
if j>=0&&j+1<b&&grid[i][j+1]=='1'{
backtrace(i,j+1)
}
if j-1>=0&&j<b&&grid[i][j-1]=='1'{
backtrace(i,j-1)
}
}
for i:=0;i<a;i++{
for j:=0;j<b;j++{
if grid[i][j]=='1'{ //找到一个岛屿,n++然后递归
n++
backtrace(i,j) //深度遍历DFS递归函数
}
}
}
return n
}
打家劫舍1 #
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
func rob( nums []int ) int {
length:=len(nums)
dp:=make([]int,length+1)
dp[1]=nums[0] //长度为1 只能偷一家
for i:=2;i<length+1;i++{
dp[i]=max(dp[i-1],dp[i-2]+nums[i-1]) //选择偷或者不偷这家的最大值
}
return dp[length]
}
func max(a,b int)int{
if a>b{
return a
}
return b
}
困难 #
买卖股票的最佳时机3 #
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
func maxProfit(prices []int) int {
n:=len(prices)
a1,b1:=-prices[0],0//只进行过一次买操作,进行了一次买操作和一次卖操作,即完成了一笔交易;
a2,b2:=-prices[0],0//在完成了一笔交易的前提下,进行了第二次买操作;完成了全部两笔交易。
for i:=1;i<n;i++{
a1=max(a1,-prices[i])
b1=max(b1,a1+prices[i])
a2=max(a2,b1-prices[i])
b2=max(b2,a2+prices[i])
}
return max(b1,max(0,b2))
}
func max(a,b int)int{
if a>b{
return a
}
return b
}
买卖股票的最佳时机4 #
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1]
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。