链表 #
链表定义 #
type ListNode struct{//单链表
Val int
Next *ListNode
}
type DoubleNode struct{//双链表
Val int
Prev *DoubleNode
Next *DoubleNode
}
创建链表 #
func CreatListNode(list []int) (tai *ListNode ){
head := &ListNode{Val: list[0]} //无头节点情况 head:=&ListNode{}
tail := head
for i := 1; i < len(list); i++ { //有头节点,这里i=0
head.Next = &ListNode{Val: list[i]}
head = head.Next
}
return tail
}
func CreatDoubleNode(list []int) (head *DoubleNode) { //创建双链表
p := &DoubleNode{}
q := p
for i := 0; i < len(list); i++ {
p.Next = &DoubleNode{Val: list[i]}
p.Next.Prev = p
p = p.Next
}
return q
}
func main() {
list := []int{1, 2, 3, 4, 5}
tail:=Creat(list)
print(tail.Next.Val)
head := CreatDoubleNode(list)
println(head.Next.Next.Val)
print(head.Next.Next.Prev.Val)
}
相关算法 #
实现单链表逆序 #
//从链表第二个节点开始,把遍历到的结点插入到头结点的后面,直到结束。
func InsertReverse(head *ListNode) {
if head == nil || head.Next == nil {
return
}
var cur *ListNode //当前结点
var next *ListNode //后继结点
cur = head.Next.Next //指向第二个结点
head.Next.Next = nil //第一结点后面断开
for cur != nil {
next = cur.Next
cur.Next = head.Next
head.Next = cur
cur = next
}
}
func reverseLinkedList(head *ListNode) {
var pre *ListNode
cur := head
for cur != nil {
next := cur.Next
cur.Next = pre
pre = cur
cur = next
}
}
从头到位输出链表 #
递归输出
func ReversPrint(head *ListNode){
if head==nil{
return
}
ReversPrint(head.Next)
Println(head.Val)
}
从无序链表中移除重复项 #
输入:head=[1,3,1,5,5,7]
输出:[1,3,5,7]
//双重循环直接在链表上操作,外层循环用一个指针从第一个节点开始遍历整个链表,然后内层循环用另外一个指针遍历其余节点,将相等结点删除。
func RemovDup(head *ListNode) *ListNode {
if head == nil {
return head
}
var pre *ListNode
pre = head
var next *ListNode
var cur *ListNode //帮助删除的前驱指针
for pre != nil {//外层循环
next = pre.Next
x := pre.Val
cur = pre
for next != nil { //内层循环
if x == next.Val { //相等就删除
cur.Next = next.Next
next = next.Next
} else { //不相等
cur = cur.Next
next = next.Next
}
}
pre = pre.Next
}
return head
}
从有序链表中移除重复项 #
输入:head = [1,1,2]
输出:[1,2]
func deleteDuplicates(head *ListNode) *ListNode {
var pre *ListNode
pre = head
var next *ListNode
if pre == nil { //排除为空情况
return head
}
for pre.Next != nil {
next = pre.Next
if pre.Val == next.Val {
pre.Next = next.Next
} else {
pre = pre.Next
}
}
return head
}
从有序链表中移除重复项2 #
输入:head = [1,2,3,3,4,4,5]
输出:[1,2,5]
//对链表中的结点直接进行相加操作,把相加的和存储到新的链表中对应的结点中,同时还要记录结点相加后的进位。
func deleteDuplicates(head *ListNode) *ListNode {
if head == nil { //排除为空
return head
}
var pre *ListNode
cur := &ListNode{-1, head} //亮点在于创建头节点 防止第一第二结点重复
pre = cur
for pre.Next != nil && pre.Next.Next != nil {
if pre.Next.Val == pre.Next.Next.Val { //如果相等了 找一个值 一个一个剔除
x := pre.Next.Val
for pre.Next != nil && pre.Next.Val == x {
pre.Next = pre.Next.Next
}
} else {
pre = pre.Next
}
}
return cur.Next
}
计算两个单链表所代表的数之和 #
输入:head1=[3,4,5,6,7,8]
head2=[9,8,7,6,5]
输出:head=[2,3,3,3,3,9]
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
dummy := &ListNode{}//定义结构体指针赋值为空
for dy,rst :=dummy,0;l1 != nil || l2 != nil || rst !=0;dy = dy.Next{
if l1 != nil {
rst += l1.Val
l1 = l1.Next
}
if l2 != nil {
rst += l2.Val
l2 = l2.Next
}
dy.Next = &ListNode{Val: rst % 10}
rst /=10
}
return dummy.Next
}
对链表进行重新排序 #
排序前:1,2,3,4,5,6,7
排序后:1,7,2,6,3,5,4
//1、先找出链表的中间节点;
//2、对链表的后半部分子链表进行逆序;
//3、把链表的前半部分子链表与逆序后的后半部分子链表进行合并
func findMiddleNode(head *ListNode) *ListNode { //找出中间节点
if head == nil && head.Next == nil {
return head
}
fast := head //快指针,每次走两步
slow := = head //慢指针,每次走一步
slowPre := head //slow的前一个指针,方便断开
for fast != nil && fast.Next != nil {
slowPre = slow
slow = slow.Next
fast = fast.Next.Next
}
slowPre.Next = nil
retrun slow
}
func reverse(head *ListNode) *ListNode { //对链表进行逆序
if head == nil && head.Next == nil {
return head
}
var pre *ListNode //前驱结点
var next *ListNode //当前结点
for head != nil {
next = head.Next
head.Next = pre
pre = head
head = next
}
return pre
}
func Reorder(head *ListNode) {
if head == nil && head.Next == nil {
return head
}
cur1 := head
mid := findMiddleNode(head)
cur2 := reverse(mid)
var tmp *ListNode
for cur.Next != nil { //合并链表
tmp = cur1.Next
cur1.Next = cur2
cur1 = tmp
tmp = cur2.Next
cur2.Next = cur1
cur2 = tmp
cur1.Next = cur2
}
}
找出单链表中倒数第K个元素 #
输入:head = [1,2,3,4,5], n = 2
输出:4
//快慢指针法
//设置两个指针,让其中一个指针比另一个指针先前移k步,然后两个指针同时向前移动,直到先行的指针为nil时,另一个指针所指位置就是要找的位置。
func FindLastK(head *ListNode, k int) *ListNode {
fast := head.Next
slow := head.Next
i := 0
for i = 0; i < k && fast != nil; i++ {
fast = fast.Next
}
if i < k { //如果i小于k 就结束 说明链遍历完了
return nil
}
for fast != nil {
slow = slow.Next
fast = fast.Next
}
return slow
}
检测一个较大单链表是否有环 * #
//快慢指针法
//慢指针前进一步,快指针前进两步,如果快指针等于慢指针,则证明这个链表有环
func IsLoop(head *ListNode) *ListNode {
fast := head
low := head
for fast != nil && fast.Next != nil {
fast = fast.Next.Next
low = low.Next
if fast == low {
return fast
}
}
return nil
}
检测一个较大单链表是否有环2 #
力扣142
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。

输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
//当发现slow与fast相遇时,我们再额外使用一个指针ptr。起始,它指向链表头部;随后,它和slow每次向后移动一个位置。最终,它们会在入环点相遇。
func detectCycle(head *ListNode) *ListNode {
if head==nil||head.Next==nil{
return nil
}
fast:=head
low:=head
for fast!=nil&&fast.Next!=nil{
fast=fast.Next.Next
low=low.Next
if fast==low{
pre:=head
for pre!=low{
pre=pre.Next
low=low.Next
}
return low
}
}
return nil
}
把链表相邻元素翻转 #
输入:[1,2,3,4,5,6,7]
输出:[2,1,4,3,6,5,7]
//力扣24题
//就地逆序,通过调整结点指针域的指向来直接调换相邻的两个结点。
func swapPairs(head *ListNode) *ListNode { //假设这里存在头结点
if head!=nil&&head.Next!=nil{
return head
}
pre:=head
cur:=head.Next
next:=head
for cur!=nil&&cur.Next!=nil{
next=cur.Next.Next //next指向第三个节点
pre.Next=cur.Next //头节点之乡第二个结点
cur.Next.Next=cur //第二个节点指向第一个结点
cur.Next=next //第一个结点指向第三个结点
pre=cur //pre 指向第一个结点 就是新链表的第二个结点
cur=next //cur 指向第三个结点 开始新的循环
}
return head
}
把链表以K个结点为一组进行翻转 #
力扣25题
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
首先把前K个结点看成一个子链表,采用前面介绍的方法进行翻转,把翻转后的子链表接到头结点后面,然后把接下来的K个结点看成另外一个单独的链表进行翻转,把翻转后的子链表接到上一个已经完成翻转子链表的后面。
func InsertReverse(head *ListNode) {//翻转子链表
if head == nil || head.Next == nil {
return head
}
var pre,next *ListNode
for head!=nil{
next=head.Next
head.Next=pre
pre=head
head=next
}
return pre
}
func reverseKGroup(head *ListNode, k int) *ListNode { //假设没有空头结点
if head ==nil||head.Next==nil{
return head
}
var begin,pre,end,pNext *ListNode
pre=&ListNode{-1,head}
begin=head
for begin!=nil{
end=begin
for i:=1;i<k;i++{
if end.Next!=nil{
end=end.Next
}else{
break
}
}
pNext=end.Next //下一个要翻转的开头
end.Next=nil //结尾断开
pre.Next=InsertReverse(begin)//翻转链表 放到pre后面
begin.Next=pNext //begin就变成了翻转后的结尾,接到pNext
pre=begin //pre 放到结尾
begin=pNext //从下一个开头开始循环
}
return head
}
翻转链表2 #
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
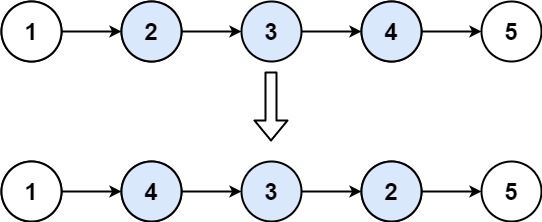
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
func reverseBetween(head *ListNode, left, right int) *ListNode {
pre:=&ListNode{-1,head}//设置头结点,防止left为1干扰
head=pre
for i:=0;i<left-1;i++{
pre=pre.Next
}
cur:=pre.Next
for i:=left;i<right;i++{ //翻转链表 直到 right
next:=cur.Next
cur.Next=next.Next
next.Next=pre.Next
pre.Next=next
}
return head.Next
}
合并两个有序链表 #
力扣21题
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
func mergeTwoLists(L1 *ListNode, L2 *ListNode) *ListNode { //叫什么归并 假设无空头结点
var head *ListNode
head=&ListNode(-1,L1) //设置头结点
pre:=head
for L1!=nil&&L2!=nil{
if L1.Val>=L2.Val{ //指向小的
pre.Next=L2
L2=L2.Next //都往后移位
pre=pre.Next
}else{
pre.Next=L1
L1=L1.Next
pre=pre.Next
}
}
//结束之后看看谁还有剩余
if L1!=nil{
pre.Next=L1
}
if L2!=nil{
pre.Next=L2
}
return head.Next
}
在只给定单链表中某个结点指针的情况下删除该结点 #
删除结点5前链表:1,2,3,4,5,6,7
删除结点5之后链表:1,2,3,4,6,7
通过把这个结点后面的数据复制到前面解决
func RemoveNode(node *ListNode) boo1 {
if node==nil||node.Next==nil{ //node为最后一个结点也完成不了
return false
}
for node.Next.Next!=nil{
node.Val=node.Next.Val
node=node.Next
}
node.Val=node.Next.Val
node.Next=nil
return true
}
判断两个单链表(无环)是否交叉 #
力扣160题
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
输入:listA = [4,1,8,4,5], listB = [5,6,1,8,4,5]
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
//首先判断链表headA和headB是否为空,如果至少一个人为空,则两个链表不相交,返回nil,当两个链表都不为空时,创建两个指针pa和pb,同时往后移,如果pa为空,pa指向headB,如果Pb为空,pb指向headA,当pa和pb指向同一个结点或者都为空时,返回他们指的结点或为nil
func getIntersectionNode(headA, headB *ListNode) *ListNode {
if headA==nil||headB==nil{
return nil
}
pa:=headA
pb:=headB
for pa!=pb { //遍历如果pa=pb=nil 退出
if pa==nil{
pa=headB
}else{
pa=pa.Next
}
if pb==nil {
pb=headA
}else{
pb=pb.Next
}
}
return pa
}
//如果两个链表相交,那么两个链表从相交点到链表结束都是相同的结点,必然是Y字型,所以,判断两个链表的最后一个结点是不是相同即可。即先遍历一个链表,直到尾部,再遍历一个链表,如果同样走到同样的尾结点,则相交,记录下链表长度n1,n2,再遍历一次,长链表先出发n1-n2步,之后同时前进,相遇的第一个结点为相交结点。
func getIntersectionNode(headA, headB *ListNode) *ListNode {
if headA==nil||headB==nil{ //假设无头结点
return nil
}
pa:=headA
pb:=headB
a,b:=1,1 //计数
for pa.Next!=nil{
pa=pa.Next
a++
}
for pb.Next!=nil{
pb=pb.Next
b++
}
if pa==pb{ //证明相交
if a>b{
n:=a-b
for i:=0;i<n;i++{
headA=headA.Next
}
for headA!=headB{
headA=headA.Next
headB=headB.Next
}
return headA
}else{
n:=b-a
for i:=0;i<n;i++{
headB=headB.Next
}
for headA!=headB{
headA=headA.Next
headB=headB.Next
}
return headA
}
}else{ //证明不相交
return nil
}
}
旋转链表 #
力扣61题
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
//先计数n,看链表有多少个元素,让后将链表变成环, 然后将头结点后移n-k%n个
func rotateRight(head *ListNode, k int) *ListNode {
}
分割链表 #
力扣86题
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
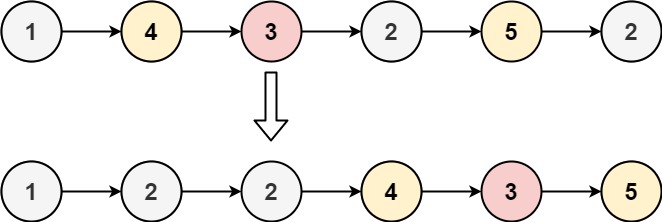
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]
//维护两个链表,large,small,遇到比x大的 放到large后面,遇到比x小的,放到small后面,然后收尾相接
func partition(head *ListNode, x int) *ListNode {
large:=&ListNode{}
small:=&ListNode{}
cur:=small
pre:=large
for head!=nil{
if head.Val<x{
small.Next=head
small=small.Next
}else{
large.Next=head
large=large.Next
}
head=head.Next
}
large.Next=nil
small.Next=pre.Next
return cur.Next
}
栈 #
栈的定义 #
/**
栈:限制插入和删除只能在一个位置上进行的表,该位置是表的末端,叫做栈的顶(top)对栈的基本操作有push(进栈)和pop(出栈)。
基本算法:
进栈(push):
1.若top>=n时,作出错误处理(进栈前先检查栈是否已满,满则溢出,不满则进入2)
2.置top = top + 1(栈指针加1,指向进栈地址)
3.s(top) = x ,结束(x为新进栈的元素)
出栈(pop):
1.若top <=0,则给出下溢信息,作出错处理(出栈前先检查栈是否为空,空则下溢,不空走2)
2.x = s(top),出栈后的元素赋值给x
3.top = top -1 ,栈指针减1,指向栈顶
*/
切片 #
// 定义常量栈的初始大小
const initSize int = 20
type Stack struct {
// 容量
size int
// 栈顶
top int
// 用slice作容器,定义为interface{}接收任意类型
data []interface{}
}
// 判断栈是否为空
func (s *Stack) IsEmpty() bool {
return s.top == -1
}
// 判断栈是否已满
func (s *Stack) IsFull() bool {
return s.top == s.size - 1
}
// 入栈
func (s *Stack) Push(data interface{}) bool {
// 首先判断栈是否已满
if s.IsFull() {
fmt.Println("stack is full, push failed")
return false
}
// 栈顶指针+1
s.top++
// 把当前的元素放在栈顶的位置
s.data[s.top] = data
return true
}
// pop,返回栈顶元素
func (s *Stack) Pop() interface{} {
// 判断是否是空栈
if s.IsEmpty() {
fmt.Println("stack is empty , pop error")
return nil
}
// 把栈顶的元素赋值给临时变量tmp
tmp := s.data[s.top]
// 栈顶指针-1
s.top--
return tmp
}
// 栈的元素的长度
func (s *Stack)GetLength() int {
length := s.top + 1
return length
}
// 清空栈
func (s *Stack) Clear() {
s.top = -1
}
// 遍历栈
func (s *Stack) Traverse() {
// 是否为空栈
if s.IsEmpty() {
fmt.Println("stack is empty")
}
for i := 0 ; i <= s.top; i++ {
fmt.Println(s.data[i], " ")
}
}
链表 #
type Node struct {
data interface{}
Next *Node
}
type Stack struct {
length int
top *Stact
}
//入栈
func (s *Stack) Push (value interface{}){
n:=&Node{value,s.top}
s.head=n
s.length++
}
//出栈
func (s *Stack) Pop interface{}{
if s.length==0{
return nil
}
n:=s.top
s.top = n.Next
s.length--
return n.data
}
实现栈 #
数组实现栈 #
// 创建并初始化栈,返回strck
func createStack() Stack {
s := Stack{}
s.size = initSize
s.top = -1
s.data = make([]interface{}, initSize)
return s
}
s1 := Stack{ //初始化栈
size: len(s),
top: -1,
data: make([]int, len(s)+1),
}
链表实现栈 #
采用头插法
相关算法 #
根据入栈序列判断可能的出栈序列 #
输入:push=[1,2,3,4,5] pop=[3,2,5,4,1]
输出:ture
思路:使用一个栈模拟入栈顺序
1.把push序列依次入栈,直到栈顶元素等于Pop序列的第一个元素,然后栈顶元素出栈,POP序列移动到第二个元素。
2.如果栈顶继续等于pop序列现在的元素,则继续出栈并pop后移,否则对push序列继续入栈。
3.如果push序列已经全部入栈,但是pop序列未全部遍历,而且栈顶元素不等于当前pop元素,那么这个序列不是一个可能的出栈序列。如果栈为空,而且pop序列也全部被遍历过,则说明这是一个可能的pop序列。
时间复杂度O(n),空间复杂度O(n)
const initSize int = 20
type Stack struct {
size int
top int
data []int
}
func (s *Stack) IsEmpty() bool { //判断栈是否为空
return s.top == -1
}
func (s *Stack) IsFull() bool { //判断栈是否已满
return s.top == s.size-1
}
func (s *Stack) Push(data int) bool {
if s.IsFull() {
return false
}
s.top++ //栈顶指针加1
s.data[s.top] = data
return true
}
func (s *Stack) Pop() int {
if s.IsEmpty() { //判断是否栈空
return -1
}
tmp := s.data[s.top]
s.top--
return tmp
}
func (s *Stack) Top() int {
if s.IsEmpty() {
return -1
}
return s.data[s.top]
}
func IsPopSerial(push []int, pop []int) bool {
pushlen := len(push)
poplen := len(pop)
if pushlen == 0 || poplen == 0 || pushlen != poplen { //判断两个长度
return false
}
s := Stack{ //初始化一个栈
size: initSize,
top: -1,
data: make([]int, initSize),
}
pushIndex := 0
popIndex := 0
for pushIndex < pushlen {
s.Push(push[pushIndex]) //push元素依次入栈 直到栈顶等于pop序列顶第一个元素
pushIndex++
for !s.IsEmpty() && s.Top() == pop[popIndex] { //栈顶元素出栈,pop序列移动到下一个元素
s.Pop()
popIndex++
}
}
if s.IsEmpty() && popIndex == poplen { //栈为空,且pop序列中元素全被遍历过
return true
}
return false
}
func main() {
push:=[]int{1,2,3,4,5}
pop:=[]int{3,4,1,2,5}
print(IsPopSerial(push,pop))
}
用O(1)的时间复杂度求栈中的最小元素 #
思路:在实现的时候采用空间换时间,使用两个栈结构,一个栈用来存储数据,另外一个栈用来存储栈的最小元素。
如果当前入栈的元素比原来栈中的最小值还小,则把这个值压入保存最小元素的栈中;在出栈的时候,如果当前出栈的元素恰好为当前栈中的最小值,则保存最小值的栈顶元素也出栈,使得当前最小值变为当前最小值入栈之前的那个最小值。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
type MinStack struct { //定义两个栈
stack *Stack
minStack *Stack
}
func (s *MinStack)Push(data int){ //入栈
s.stack.Push(data) //普通栈首先先入
if s.minStack.IsEmpty(){ //保存最小值的栈 如果空则入
s.minStack.Push(data)
}else{
if data<=s.minStack.Top(){ //不为空比较一下 再入
s.minStack.Push(data)
}
}
}
func (p *MinStack)Pop()int { //出栈
topData:=p.stack.Pop() //普通栈直接出
if topData==p.Min(){ //如果出的是最小值,则保存最小值的栈 出栈
p.minStack.Pop()
}
return topData
}
func (p * MinStack)Min()int {
if p.minStack.IsEmpty(){ //如果为空,返回一个特定值
return math.MaxInt32
}else{
return p.minStack.Top() //不为空返回栈顶元素
}
}
用两个栈模拟队列 #
思路:A为插入栈,B为弹出栈。
如果栈B不为空,则直接弹出栈B的数据。
如果栈B为空,则一次弹出栈A的数据,放入B中,再弹出栈B的数据。
type StackQueue struct{ //定义两个栈
aStack *Stack
bStack *Stack
}
func (s *StackQueue) Push (data int) { //只有a入栈
s.aStack.Push(data)
}
func (s *StackQueue) Pop () int{
if s.bStack.IsEmpty() { //b为空,弹出a的数据放入b,再弹出栈b数据
for !s.aStack.IsEmpty(){
s.bStack.Push(s.aStack.Pop())
}
}
return s.bStack.Pop() //b不为空直接弹出
}
队列 #
定义 #
切片 #
type queue struct {
data []int
front int //队头
rear int //队尾
}
//判断队列是否为空
func (s *queue) IsEmpty() bool {
return s.front == s.rear
}
//返回队列大小
func (s *queue) Size() int {
return s.rear - s.front
}
//返回队列首元素
func (s *queue) GetFront() int {
if s.IsEmpty() {
panic(errors.New("队列为空"))
}
return s.data[s.front]
}
//返回队尾元素
func (s *queue) GetBack() int {
if s.IsEmpty() {
panic(errors.New("队列为空"))
}
return s.data[s.rear-1]
}
//删除队列头元素
func (s *queue) DeQueue() {
if s.rear > s.front {
s.rear--
s.data = s.data[1:]
} else {
panic(errors.New("队列为空"))
}
}
//把新元素加入队列尾
func (s *queue) EnQueue(item int) {
s.data = append(s.data, item)
s.rear++
}
链表 #
type ListNode struct { //单链表
Val int
Next *ListNode
}
type LinkQueue struct {
head *ListNode
end *ListNode
}
//判断队列是否为空
func (s *LinkQueue) IsEmpty() bool {
return s.head == nil
}
//获取队列中元素个数
func (s *LinkQueue) Size() int {
size := 0
node := s.head
for node != nil {
node = node.Next
size++
}
return size
}
//入队列,队尾入
func (s *LinkQueue) EnQueue(temp int) {
node := &ListNode{Val: temp}
if s.head == nil {
s.head = node
s.end = node
} else {
s.end.Next = node
s.end = node
}
}
//出队列,对头出
func (s *LinkQueue) DeQueue() {
if s.head == nil {
panic(errors.New("队列为空"))
}
s.head = s.head.Next
if s.head == nil {
s.end = nil
}
}
//取得队列首元素
func (s *LinkQueue) GetFront() int {
if s.head == nil {
panic(errors.New("队列为空"))
}
return s.head.Val
}
//取得队列尾元素
func (s *LinkQueue) GetBack() int {
if s.end == nil {
panic(errors.New("队列为空"))
}
return s.end.Val
}
实现队列 #
切片 #
func CreatQueue() queue { //初始化一个队列
s := queue{}
s.rear = 0
s.front = 0
s.data = make([]int, 0)
return s
}
s := queue{
rear: 0,
front: 0,
data: make([]int, 0),
}
链表 #
s:=&LinkQueue{}
相关算法 #
用队列实现栈 #
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
思路:一个队列实现栈,队列为空,直接入队,队列不为空,入队,前面的全部出队再入队。
type MyStack struct {
stack *queue
}
func Constructor() (s MyStack) { //定义栈
return
}
func (this *MyStack) Push(x int) {
n:=this.stack.Size
this.stack.EnQueue(x)
for ; n>0;n--{
c:=this.stack.GetFront //得到队头元素
this.stack.EnQueue(c) //插入队尾
this.stack.DeQueue //删除队头
}
}
func (this *MyStack) Pop() int {
a:=this.stack.GetBack
this.stack.DeQueue
return a
}
func (this *MyStack) Top() int {
return this.stack.GetFront
}
func (this *MyStack) Empty() bool {
return this.stack.IsEmpty
}
实现LRU缓存方案 #
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
* 使用双向链表实现的队列,队列的最大容量为缓存的大小。在使用的过程中,把最近使用的页面移动到队列首,最近没有使用使用的页面将被放在队列尾的位置。
* 使用一个哈希表,把页号作为键,把缓存在队列中的结点的地址作为值。
当引用一个页面时,所需的页面在内存中,我们需要把这个页对应的结点移动到队列的前面。如果所需的页面不在内存中,我们将它存储在内存中。简单地说,就是将一个新结点添加到队列的前面,并在哈希表中更新相应的结点地址。如果队列是满的,那么就从队列尾部移除一个结点,并将新结点添加到队列的前面。
//很烦直接复制粘贴了
type LRUCache struct {
size int
capacity int
cache map[int]*DLinkedNode
head, tail *DLinkedNode
}
type DLinkedNode struct {
key, value int
prev, next *DLinkedNode
}
func initDLinkedNode(key, value int) *DLinkedNode {
return &DLinkedNode{
key: key,
value: value,
}
}
func Constructor(capacity int) LRUCache {
l := LRUCache{
cache: map[int]*DLinkedNode{},
head: initDLinkedNode(0, 0),
tail: initDLinkedNode(0, 0),
capacity: capacity,
}
l.head.next = l.tail
l.tail.prev = l.head
return l
}
func (this *LRUCache) Get(key int) int {
if _, ok := this.cache[key]; !ok {
return -1
}
node := this.cache[key]
this.moveToHead(node)
return node.value
}
func (this *LRUCache) Put(key int, value int) {
if _, ok := this.cache[key]; !ok {
node := initDLinkedNode(key, value)
this.cache[key] = node
this.addToHead(node)
this.size++
if this.size > this.capacity {
removed := this.removeTail()
delete(this.cache, removed.key)
this.size--
}
} else {
node := this.cache[key]
node.value = value
this.moveToHead(node)
}
}
func (this *LRUCache) addToHead(node *DLinkedNode) {
node.prev = this.head
node.next = this.head.next
this.head.next.prev = node
this.head.next = node
}
func (this *LRUCache) removeNode(node *DLinkedNode) {
node.prev.next = node.next
node.next.prev = node.prev
}
func (this *LRUCache) moveToHead(node *DLinkedNode) {
this.removeNode(node)
this.addToHead(node)
}
func (this *LRUCache) removeTail() *DLinkedNode {
node := this.tail.prev
this.removeNode(node)
return node
}
二叉树 #
定义 #
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
实现 #
//设置结点的值
func (node *TreeNode) SetValue(value int) {
node.Val = value
}
//创建结点
func CreatNode(value int) *TreeNode {
return &TreeNode{value, nil, nil}
}
//递归查找结点
func (node *TreeNode) FindNode(n *TreeNode, x int) *TreeNode {
if n == nil {
return nil
} else if n.Val == x {
return n
} else {
p := node.FindNode(n.Left, x)
if p != nil {
return p
}
return node.FindNode(n.Right, x)
}
}
//递归求树的高度
//对于任意一个子树的根节点来说,它的深度=左右子树深度的最大值+1
func (node *TreeNode) GetTreeHeigh(n *TreeNode) int {
if n == nil {
return 0
} else {
lHeigh := node.GetTreeHeigh(n.Left)
rHeigh := node.GetTreeHeigh(n.Right)
if lHeigh > rHeigh {
return lHeigh + 1
} else {
return rHeigh + 1
}
}
}
//非递归求树的高度
//借助队列,在进行层次遍历时,记录遍历的层数
func (node *TreeNode) GetTreeHeigh2() int {
if node == nil {
return 0
}
layers := 0
nodes := []*TreeNode{node}
for len(nodes) > 0 {
layers++
size := len(nodes) //每层的结点树
count := 0
for count < size {
count++
curNode := nodes[0]
nodes = nodes[1:]
if curNode.Left != nil {
nodes = append(nodes, curNode.Left)
}
if curNode.Right != nil {
nodes = append(nodes, curNode.Right)
}
}
}
return layers
}
//递归前序遍历二叉树
func (node *TreeNode) PreOrder(n *TreeNode) {
if n != nil {
print("%d", n.Val)
node.PreOrder(n.Left)
node.PreOrder(n.Right)
}
}
//递归中序遍历二叉树
func (node *TreeNode) InOrder(n *TreeNode) {
if n != nil {
node.InOrder(n.Left)
print("%d", n.Val)
node.InOrder(n.Right)
}
}
//递归后序遍历二叉树
func (node *TreeNode) PostOrder(n *TreeNode) {
if n != nil {
node.PostOrder(n.Left)
node.PostOrder(n.Right)
print("%d", n.Val)
}
}
//层次遍历(广度优先遍历)
func (node *TreeNode) BreadthFirstSearch() {
if node == nil {
return
}
result := []int{} //创建队列
nodes := []*TreeNode{node}
for len(nodes) > 0 {
curNode := nodes[0] //访问结点
nodes = nodes[1:]
result = append(result, curNode.Val) //入队
if curNode.Left != nil {
nodes = append(nodes, curNode.Left)
}
if curNode.Right != nil {
nodes = append(nodes, curNode.Right)
}
}
for _, v := range result {
print(v)
}
}
//创建一颗树
func main() {
root := CreateNode(5)
root.left = CreateNode(2)
root.right = CreateNode(4)
root.left.right = CreateNode(7)
root.left.right.left = CreateNode(6)
root.right.left = CreateNode(8)
root.right.right = CreateNode(9)
}
相关算法 #
B树和B+树 #
图 #
查找 #
相关算法 #
二分查找1 #
请实现无重复数字的升序数组的二分查找
给定一个 元素升序的、无重复数字的整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标(下标从 0 开始),否则返回 -1
输入:[-1,0,3,4,6,10,13,14],13
返回值:6
func search( nums []int , target int ) int {
left,right:=0,len(nums)-1
mid:=0
for left<=right{
mid=left+(right-left)/2 //二分查找精髓
if nums[mid]==target{
return mid
}
if nums[mid]>target{
right=mid-1
}else{
left=mid+1
}
}
return -1
}
二维数组中的查找 #
在一个二维数组array中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1,2,8,9], [2,4,9,12], [4,7,10,13], [6,8,11,15]
]
给定 target = 7,返回 true。
给定 target = 3,返回 false。
数据范围:矩阵的长宽满足 0≤n,m≤5000≤n,m≤500 , 矩阵中的值满足 0≤val≤1090≤val≤109 进阶:空间复杂度 O(1)O(1) ,时间复杂度 O(n+m)O(n+m)
示例1
输入:
7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值:true
func Find( target int , array [][]int ) bool { //关键在于左边的比你小,你下面的比你大,故从右上开始
m,n:=len(array),len(array[0])
for i,j:=0,n-1;i<m&&j>=0;{
if array[i][j]==target{
return true
}
if array[i][j]>target{ //往左下查找
j--
}else{
i++
}
}
return false
}
并查集 #
并查集是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
顾名思义,并查集支持两种操作:
- 合并(Union):合并两个元素所属集合(合并对应的树)
- 查询(Find):查询某个元素所属集合(查询对应的树的根节点),这可以用于判断两个元素是否属于同一集合
并查集在经过修改后可以支持单个元素的删除、移动;使用动态开点线段树还可以实现可持久化并查集。
初始化 #
初始时,每个元素都位于一个单独的集合,表示为一棵只有根节点的树。方便起见,我们将根节点的父亲设为自己。

type UnionFind struct {
parent []int
}
func NewUnionFind(n int) *UnionFind {
uf := new(UnionFind)
uf.parent = make([]int, n)
for i := 0; i < n; i++ {
uf.parent[i] = i
}
return uf
}
查找 #
我们需要沿着树向上移动,直至找到根节点。
func (uf *UnionFind) find(x int) int {
if uf.parent[x] != x {
uf.parent[x] = uf.find(uf.parent[x])//让当前节点不断等于它的父节点
}
return uf.parent[x]
}
//非路径压缩版
func (uf *UnionFind) find2(x int) int {
for {
if uf.parent[x] != x {
x = uf.parent[x]//让x=数组中的值,下一次循环查它的父节点
} else {
return uf.parent[x]
}
}
}
func (uf *UnionFind) find2(x int) int {
if uf.parent[x] == x {
return uf.parent[x]
}
return uf.find(uf.parent[x])
}
合并 #
要合并两棵树,我们只需要将一棵树的根节点连到另一棵树的根节点。

func (uf *UnionFind) union(x, y int) {
x, y = uf.find(x), uf.find(y) //查找根节点
if x == y { //同一棵树
return
}
if x > y { //// 总是让字典序更小的作为集合代表字符 根据情况,也可以换成最大的或者不换
x, y = y, x
}
uf.parent[y] = x
}
相关算法 #
堆 #
排序 #
算法比较 #
| 排序方法 | 最好时间 | 平均时间 | 最坏时间 | 辅助存储 | 稳定性 | 备注 |
|---|---|---|---|---|---|---|
| 简单选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 | n小时较好 |
| 直接插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 | 大部分已有序时较好 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 | n小时较好 |
| 希尔排序 | O(N) | O(nlogn) | O(ns)1<s<2 | O(1) | 不稳定 | s是所选分组 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(logn) | 不稳定 | n大时较好 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 | n大时较好 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 | n大时较好 |
虽然直接插入排序和冒泡排序的速度比较慢,但是当初始序列整体或局部有序时,这两种排序算法会有比较好的效率。当初始序列整体或局部有序时,快速排序算法的效率会下降。当排序序列较小且不要求稳定时,直接选择排序效率好;要求稳定时,冒泡排序效率较好。
堆排序、快速排序的时间复杂度以及分别适用什么场景 #
当数据规模较大时,应用速度最快的排序算法,可以考虑使用快速排序。
快速排序平均时间复杂度:O(nlogn)
快速排序最好时间复杂度:O(nlogn)
快速排序平均空间复杂度:O(logn)
堆排序不会出现快排那样最坏情况,且堆排序所需的辅助空间比快排要少,但是这两种算法都不是稳定的,要求排序时是稳定的,可以考虑用归并排序。
堆排序平均时间复杂度:**O(n*logn)**空间复杂度几乎为0(只用到几个临时变量)
对记录较少的文件效果一般,对于记录较多的文件很有效,其运行时间主要耗费在创建堆和反复调整堆上。
(1)当数据规模较小时候,可以使用简单的直接插入排序或者直接选择排序。
(2)当文件的初态已经基本有序,可以用直接插入排序和冒泡排序。
(3)当数据规模较大时,应用速度最快的排序算法,可以考虑使用快速排序。当记录随机分布的时候,快速排序平均时间最短,但是出现最坏的情况,这个时候的时间复杂度是O(n^2),且递归深度为n,所需的占空间为O(n)。
(4)堆排序不会出现快排那样最坏情况,且堆排序所需的辅助空间比快排要少,但是这两种算法都不是稳定的,要求排序时是稳定的,可以考虑用归并排序。
(5)归并排序可以用于内部排序,也可以使用于外部排序。在外部排序时,通常采用多路归并,并且通过解决长顺串的合并,缠上长的初始串,提高主机与外设并行能力等,以减少访问外存额外次数,提高外排的效率。
选择排序 #
[3 4 2 1 7 6 8 9 5 0]*
[0 4 2 1 7 6 8 9 5 3]
[0 1 2 4 7 6 8 9 5 3]
[0 1 2 3 7 6 8 9 5 4]
...
[0 1 2 3 4 5 6 7 8 9]
平均时间复杂度:O(n^2)
空间复杂度:O(1)
代码 #
func SelectSort(data []int) {
l := len(data) //得到数组长度
for i := 0; i < l; i++ {
tmp := i //定位
for j := i + 1; j < l; j++ {
if data[tmp] >= data[j] {
tmp = j //定位到最小值下标
}
}
data[i], data[tmp] = data[tmp], data[i] //交换
}
}
func main() {
data := []int{0, 0, 0, 0, 0, 0}
SelectSort(data)
fmt.Println(data)
}
插入排序 #
[3 4 2 1 7 6 8 9 5 0]*
[3 4 2 1 7 6 8 9 5 0]
[3 4 2 1 7 6 8 9 5 0]
[2 3 4 1 7 6 8 9 5 0]
[1 2 3 4 7 6 8 9 5 0]
...
[0 1 2 3 4 5 6 7 8 9]
平均时间复杂度:O(n^2)
空间复杂度:O(1)
代码 #
func InsertSort(data []int) {
if data == nil { //如果为空返回
return
}
for i := 1; i < len(data); i++ { //默认从第二个开始
tmp := 0
for j := tmp; j < i; j++ {
if data[i] < data[j] { //发现后面的小,开始交换 否则j++到i
data[j], data[i] = data[i], data[j] //交换
}
}
}
}
func main() {
data := []int{5, 4, 1, 1, 0, 5, 0}
InsertSort(data)
fmt.Println(data)
}
冒泡排序 #
[3 4 2 1 7 6 8 9 5 0]*
[3 2 1 4 6 7 8 5 0 9]
[2 1 3 4 6 7 5 0 8 9]
[1 2 3 4 6 5 0 7 8 9]
...
[0 1 2 3 4 5 6 7 8 9]
平均时间复杂度:O(n^2)
空间复杂度:O(1)
代码 #
func BubbleSort(data []int) {
l := len(data)
for i := 0; i < l-1; i++ {
for j := 0; j < l-1-i; j++ { //每次循环都会有一个数值到达指定位置,故j<l-1-i 无需后面比较
if data[j] > data[j+1] {
data[j], data[j+1] = data[j+1], data[j]
}
}
}
}
func main() {
data := []int{5, 4, 3, 1, 0}
BubbleSort(data)
fmt.Println(data)
}
归并排序 #
[3 4 2 1 7 6 8 9 5 0]*
[3 4][1 2][6 7][8 9][0 5]
[1 2 3 4][6 7 8 9][0 5]
[1 2 3 4 6 7 8 9][0 5]
[0 1 2 3 4 5 6 7 8 9]
二路归并过程需要进行logn趟。每一趟归并操作,就是将两个有序子序列进行归并,而每一对有序子序列归并时,记录的比较次数均小于等于记录的移动次数,记录移动的次数均等于文件中记录的个数n,即每一趟归并的时间复杂度为O(n)
平均时间复杂度:O(nlogn)
空间复杂度:O(n)
代码 #
// 自顶向下归并排序,排序范围在 [begin,end) 的数组
func MergeSort(array []int, begin int, end int) {
// 元素数量大于1时才进入递归
if end - begin > 1 {
// 将数组一分为二,分为 array[begin,mid) 和 array[mid,high)
mid := begin + (end-begin+1)/2
// 先将左边排序好
MergeSort(array, begin, mid)
// 再将右边排序好
MergeSort(array, mid, end)
// 两个有序数组进行合并
merge(array, begin, mid, end)
}
}
// 归并操作
func merge(array []int, begin int, mid int, end int) {
// 申请额外的空间来合并两个有序数组,这两个数组是 array[begin,mid),array[mid,end)
leftSize := mid - begin // 左边数组的长度
rightSize := end - mid // 右边数组的长度
newSize := leftSize + rightSize // 辅助数组的长度
result := make([]int, 0, newSize)
l, r := 0, 0
for l < leftSize && r < rightSize {
lValue := array[begin+l] // 左边数组的元素
rValue := array[mid+r] // 右边数组的元素
// 小的元素先放进辅助数组里
if lValue < rValue {
result = append(result, lValue)
l++
} else {
result = append(result, rValue)
r++
}
}
// 将剩下的元素追加到辅助数组后面
result = append(result, array[begin+l:mid]...)
result = append(result, array[mid+r:end]...)
// 将辅助数组的元素复制回原数组,这样该辅助空间就可以被释放掉
for i := 0; i < newSize; i++ {
array[begin+i] = result[i]
}
return
}
希尔排序 #
通常间隔为总长度的一半
[3 4 2 1 7 6 8 9 5 0]*
[3 4 2 1 0 6 8 9 5 7]5
[0 1 2 4 3 6 5 7 8 9]2
[0 1 2 3 4 5 6 7 8 9]1
希尔排序的关键并不是随便地分组后各自排序,而是将相隔某个“增量”的记录组成一个子序列,实现跳跃式地移动,使得排序的效率提高。
平均时间复杂度:O(n*logn)
空间复杂度:O(1)
代码 #
func ShellSort(data []int) {
for gap := len(data) / 2; gap > 0; gap = gap / 2 {// 进行分组
for i := gap; i < len(data); i++ {// i 待排序的元素 // 插入排序
for j := i; j >= gap; j = j - gap {// j 在比较过程中, 待排序元素的位置
if data[j-gap] <= data[j] {// 同组左边的元素 <= 待排序元素
break
}
data[j-gap], data[j] = data[j], data[j-gap]// 交换
}
}
}
}
func main() {
data := []int{5, 4, 3, 1, 0}
ShellSort(data)
fmt.Println(data)
}
堆排序 #
平均时间复杂度:O(n*logn)
空间复杂度几乎为0(只用到几个临时变量)
对记录较少的文件效果一般,对于记录较多的文件很有效,其运行时间主要耗费在创建堆和反复调整堆上。
即使在最坏情况下,其时间复杂度也为O(n*logn)。
堆排序主要包括两个过程:一是构建堆;二是交换堆顶元素与最后一个元素的位置。
具有n个结点的完全二叉树深度为(log2n)+1,其中(log2n)+1是向下取整。
完全二叉树性质:
下标为i的结点的父结点下标:(i-1)/2
下标为i的结点的左孩子结点下标:i*2+1
下标为i的结点的右孩子结点下标:i*2+2
代码 #
func HeapSort(arr []int) []int {
length := len(arr)
for i := 0; i < length; i++ {
lastmesslen := length - i //长度减1缩短堆大小,最后端元素位置定型
HeapScortMax(arr, lastmesslen) //调整堆
//fmt.Println(arr)
if i < length { //将最前面的跟最后面的换一下
arr[0], arr[lastmesslen-1] = arr[lastmesslen-1], arr[0]
}
//fmt.Println("ex", arr)
}
return arr
}
func HeapScortMax(arr []int, length int) []int {
//length := len(arr)
if length <= 1 {
return arr
} else {
depth := length/2 - 1 //节点下标,n,2*n+1,2*n+2 最大父节点下标
for i := depth; i >= 0; i-- {
topmax := i //指向父结点
left := 2*i + 1 //左孩子下标
right := 2*i + 2 //右孩子下标
if left <= length-1 && arr[left] < arr[topmax] { //防止越界 这里< 输出由大到小
topmax = left //定位
}
if right <= length-1 && arr[right] < arr[topmax] { //注意topmax >输出由小到大
topmax = right
}
if topmax != i { //如果topmax发生变化交换位置
arr[i], arr[topmax] = arr[topmax], arr[i]
}
}
return arr
}
}
func main() {
arr := []int{15, 21, 0, 23, 8, -1}
fmt.Print(HeapSort(arr))
}
快速排序 #
快速排序采用分而治之的思想
每次排序均有一个数字到达其最终位置,左边均比其小,右边均比其大。
当数据规模较大时,应用速度最快的排序算法,可以考虑使用快速排序。
最坏时间复杂度:O(n^2)
平均时间复杂度:O(nlogn)
最好时间复杂度:O(nlogn)
平均空间复杂度:O(logn)
对于一组给定的记录,通过一趟排序后,将原序列分为两部分,其中前一部分的所有记录均比后一部分的所有记录小,然后再依次对前后两部分的记录进行快速排序,递归该过程,直到序列中的所有记录均有序为止。
代码 #
func sort(arry []int, left, right int) { //数组,左右下标
if left >= right {
return
}
i := left
j := right
temp := arry[i] //用于交换值
for i < j {
for i < j && arry[j] > temp { //从后往前 如过后面的大于前面的 则j--
j--
}
if i < j { //到这里证明arry[i]>=arry[j]
arry[i] = arry[j] //让arry[i]=arry[j]
i++ //向后移
}
for i < j && arry[i] < temp {
i++
}
if i < j { //到这里证明arry[i]>=temp
arry[j] = arry[i]
j--
}
}
arry[i] = temp
sort(arry, left, i-1) //左右放入递归
sort(arry, i+1, right)
}
func QuickSort(arry []int) {
sort(arry, 0, len(arry)-1)
}
func main() {
data := []int{5, 4, 9, 8, 7, 6, 0, 1, 3, 2}
QuickSort(data)
fmt.Println(data)
}