简单 #
旅行终点站 #
给你一份旅游线路图,该线路图中的旅行线路用数组 paths 表示,其中 paths[i] = [cityAi, cityBi] 表示该线路将会从 cityAi 直接前往 cityBi 。请你找出这次旅行的终点站,即没有任何可以通往其他城市的线路的城市*。*
题目数据保证线路图会形成一条不存在循环的线路,因此恰有一个旅行终点站。
输入:paths = [["B","C"],["D","B"],["C","A"]]
输出:"A"
解释:所有可能的线路是:
"D" -> "B" -> "C" -> "A".
"B" -> "C" -> "A".
"C" -> "A".
"A".
显然,旅行终点站是 "A" 。
func destCity(paths [][]string) string { //合并区间
for i, j := 0, 1; j < len(paths); {
if len(paths) == 1 {
break
}
if paths[i][1] == paths[j][0] {
paths[i][1] = paths[j][1]
paths = append(paths[:j], paths[j+1:]...)
j = 1
continue
}
if paths[i][0] == paths[j][1] {
paths[j][1] = paths[i][1]
paths = append(paths[:i], paths[i+1:]...)
j = 1
continue
}
j++
}
return paths[0][1]
}
官方:
func destCity(paths [][]string) string {
citiesA := map[string]bool{}
for _, path := range paths { //每个开始都给true
citiesA[path[0]] = true
}
for _, path := range paths {
if !citiesA[path[1]] { //如果没有则证明是最后一个
return path[1]
}
}
return ""
}
求出出现两次数字的XOR值 #
给你一个数组 nums ,数组中的数字 要么 出现一次,要么 出现两次。
请你返回数组中所有出现两次数字的按位 XOR 值,如果没有数字出现过两次,返回 0 。
示例 1:
**输入:**nums = [1,2,1,3]
**输出:**1
解释:
nums 中唯一出现过两次的数字是 1 。
示例 2:
**输入:**nums = [1,2,3]
**输出:**0
解释:
nums 中没有数字出现两次。
示例 3:
**输入:**nums = [1,2,2,1]
**输出:**3
解释:
数字 1 和 2 出现过两次。1 XOR 2 == 3 。
func duplicateNumbersXOR(nums []int) int {
cMap:=make(map[int]struct{},0)
number:=0
for _,num:=range nums{
if _,ok:=cMap[num];ok{
number=number^num
}else{
cMap[num]=struct{}{}
}
}
return number
}
官方:
func duplicateNumbersXOR(nums []int) int {
cnt := make(map[int]bool)
res := 0
for _, num := range nums {
if _, found := cnt[num]; found {
res ^= num
} else {
cnt[num] = true
}
}
return res
}
字母在字符串中的百分比 #
给你一个字符串 s 和一个字符 letter ,返回在 s 中等于 letter 字符所占的 百分比 ,向下取整到最接近的百分比。
示例 1:
输入:s = "foobar", letter = "o"
输出:33
解释:
等于字母 'o' 的字符在 s 中占到的百分比是 2 / 6 * 100% = 33% ,向下取整,所以返回 33 。
func percentageLetter(s string, letter byte) int {
count:=0
for _,v:=range []byte(s){
if v==letter{
count++
}
}
return int(float64(count) / float64(len(s))* 100)
}
遇到的坑 #
-
float32(59) / float32(100)的精确数学结果是0.59。 -
但
float32是 32位单精度浮点数,其有效位数约为 7位十进制数字,无法精确表示0.59。 -
实际存储的值可能是近似值,例如
0.58999997(因二进制浮点数无法精确表示某些十进制小数)。 -
继续计算
0.58999997 * 100,结果是58.999997(而非精确的59.0)。 -
Go 的
int(...)会直接 截断小数部分(不是四舍五入)。 -
int(58.999997) → 58。
奇偶频次间的最大差值 I #
给你一个由小写英文字母组成的字符串 s 。
请你找出字符串中两个字符 a1 和 a2 的出现频次之间的 最大 差值 diff = a1 - a2,这两个字符需要满足:
a1在字符串中出现 奇数次 。a2在字符串中出现 偶数次 。
返回 最大 差值。
示例 1:
**输入:**s = “aaaaabbc”
**输出:**3
解释:
- 字符
'a'出现 奇数次 ,次数为5;字符'b'出现 偶数次 ,次数为2。 - 最大差值为
5 - 2 = 3。
示例 2:
**输入:**s = “abcabcab”
**输出:**1
解释:
- 字符
'a'出现 奇数次 ,次数为3;字符'c'出现 偶数次 ,次数为 2 。 - 最大差值为
3 - 2 = 1。
func maxDifference(s string) int {
cnt:=make(map[rune]int)
for _,v:=range s{
if value,ok:=cnt[v];ok{
value++
cnt[v]=value
}else{
cnt[v]=1
}
}
maxOdd,minEven:=1,len(s)
for _,v:=range cnt{
if v%2==1{
maxOdd=max(maxOdd,v)
}else{
minEven=min(minEven,v)
}
}
return maxOdd-minEven
}
仅含置位位的最小整数 #
给你一个正整数 n。
返回 大于等于 n 且二进制表示仅包含 置位 位的 最小 整数 x 。
置位 位指的是二进制表示中值为 1 的位。
示例 1:
输入: n = 5
输出: 7
**解释:**7 的二进制表示是 "111"。
示例 2:
输入: n = 10
输出: 15
**解释:**15 的二进制表示是 "1111"。
示例 3:
输入: n = 3
输出: 3
**解释:**3 的二进制表示是 "11"。
func smallestNumber(n int) int {
for i:=0;;i++{
if (2<<i-1)>=n{ 2*2^i -1
return 2<<i-1
}
}
}
数字小镇中的捣蛋鬼 #
数字小镇 Digitville 中,存在一个数字列表 nums,其中包含从 0 到 n - 1 的整数。每个数字本应 只出现一次,然而,有 两个 顽皮的数字额外多出现了一次,使得列表变得比正常情况下更长。
为了恢复 Digitville 的和平,作为小镇中的名侦探,请你找出这两个顽皮的数字。
返回一个长度为 2 的数组,包含这两个数字(顺序任意)。
示例 1:
输入: nums = [0,1,1,0]
输出: [0,1]
**解释:**数字 0 和 1 分别在数组中出现了两次。
示例 2:
输入: nums = [0,3,2,1,3,2]
输出: [2,3]
解释: 数字 2 和 3 分别在数组中出现了两次。
func getSneakyNumbers(nums []int) []int {
result:=make([]int,0)
m:=make(map[int]struct{})
for _,i:=range nums{
if _,ok:=m[i];ok{
result=append(result,i)
}else{
m[i]=struct{}{}
}
}
return result
}
使数组元素等于零 #
给你一个整数数组 nums 。
开始时,选择一个满足 nums[curr] == 0 的起始位置 curr ,并选择一个移动 方向 :向左或者向右。
此后,你需要重复下面的过程:
- 如果
curr超过范围[0, n - 1],过程结束。 - 如果
nums[curr] == 0,沿当前方向继续移动:如果向右移,则 递增curr;如果向左移,则 递减curr。 - 如果
nums[curr] > 0:- 将
nums[curr]减 1 。 - 反转 移动方向(向左变向右,反之亦然)。
- 沿新方向移动一步。
- 将
如果在结束整个过程后,nums 中的所有元素都变为 0 ,则认为选出的初始位置和移动方向 有效 。
返回可能的有效选择方案数目。
示例 1:
**输入:**nums = [1,0,2,0,3]
**输出:**2
**解释:**可能的有效选择方案如下:
- 选择
curr = 3并向左移动。[1,0,2,**0**,3] -> [1,0,**2**,0,3] -> [1,0,1,**0**,3] -> [1,0,1,0,**3**] -> [1,0,1,**0**,2] -> [1,0,**1**,0,2] -> [1,0,0,**0**,2] -> [1,0,0,0,**2**] -> [1,0,0,**0**,1] -> [1,0,**0**,0,1] -> [1,**0**,0,0,1] -> [**1**,0,0,0,1] -> [0,**0**,0,0,1] -> [0,0,**0**,0,1] -> [0,0,0,**0**,1] -> [0,0,0,0,**1**] -> [0,0,0,0,0].
- 选择
curr = 3并向右移动。[1,0,2,**0**,3] -> [1,0,2,0,**3**] -> [1,0,2,**0**,2] -> [1,0,**2**,0,2] -> [1,0,1,**0**,2] -> [1,0,1,0,**2**] -> [1,0,1,**0**,1] -> [1,0,**1**,0,1] -> [1,0,0,**0**,1] -> [1,0,0,0,**1**] -> [1,0,0,**0**,0] -> [1,0,**0**,0,0] -> [1,**0**,0,0,0] -> [**1**,0,0,0,0] -> [0,0,0,0,0].
示例 2:
**输入:**nums = [2,3,4,0,4,1,0]
**输出:**0
**解释:**不存在有效的选择方案。
//若左右两侧和相等,ans+=2;若左右两侧和差一,ans++
func countValidSelections(nums []int) int {
res:=0
m:=0
for i:=0;i<len(nums);i++{
m+=nums[i]
if nums[i]==0{
n:=0
for j:=i;j<len(nums);j++{
n+=nums[j]
}
if m==n{
res+=2
}
if m-n==1||n-m==1{
res++
}
}
}
return res
}
func countValidSelections(nums []int) int {
n := len(nums)
sum := 0
for _, x := range nums { //先求出总和
sum += x
}
ans, leftSum, rightSum := 0, 0, sum
for i := 0; i < n; i++ {
if nums[i] == 0 { //一次遍历求差值
if leftSum-rightSum >= 0 && leftSum-rightSum <= 1 {
ans++
}
if rightSum-leftSum >= 0 && rightSum-leftSum <= 1 {
ans++
}
} else { //左边相加 右边减掉
leftSum += nums[i]
rightSum -= nums[i]
}
}
return ans
}
计算字数组的x-sum 1 #
给你一个由 n 个整数组成的数组 nums,以及两个整数 k 和 x。
数组的 x-sum 计算按照以下步骤进行:
- 统计数组中所有元素的出现次数。
- 仅保留出现频率最高的前
x种元素。如果两种元素的出现次数相同,则数值 较大 的元素被认为出现次数更多。 - 计算结果数组的和。
注意,如果数组中的不同元素少于 x 个,则其 x-sum 是数组的元素总和。
返回一个长度为 n - k + 1 的整数数组 answer,其中 answer[i] 是 子数组 nums[i..i + k - 1] 的 x-sum。
子数组 是数组内的一个连续 非空 的元素序列。
示例 1:
**输入:**nums = [1,1,2,2,3,4,2,3], k = 6, x = 2
输出:[6,10,12]
解释:
- 对于子数组
[1, 1, 2, 2, 3, 4],只保留元素 1 和 2。因此,answer[0] = 1 + 1 + 2 + 2。 - 对于子数组
[1, 2, 2, 3, 4, 2],只保留元素 2 和 4。因此,answer[1] = 2 + 2 + 2 + 4。注意 4 被保留是因为其数值大于出现其他出现次数相同的元素(3 和 1)。 - 对于子数组
[2, 2, 3, 4, 2, 3],只保留元素 2 和 3。因此,answer[2] = 2 + 2 + 2 + 3 + 3。
示例 2:
**输入:**nums = [3,8,7,8,7,5], k = 2, x = 2
输出:[11,15,15,15,12]
**解释:**由于 k == x,answer[i] 等于子数组 nums[i..i + k - 1] 的总和。
func findXSum(nums []int, k int, x int) []int {
n := len(nums)
answer := make([]int, n-k+1)
for i := 0; i < n-k+1; i++ {
answer[i] = getSum(nums[i:i+k], x)
}
return answer
}
func getSum(nums []int, x int) int {
xCount := make(map[int]int)
// 统计每个数字出现的次数
for i := 0; i < len(nums); i++ {
if _, ok := xCount[nums[i]]; ok {
xCount[nums[i]] = xCount[nums[i]] + 1
} else {
xCount[nums[i]] = 1
}
}
// 将 map 转换为键值对切片并按键(数字)降序排序
type kv struct {
Key int
Value int
}
var pairs []kv
for k, v := range xCount {
pairs = append(pairs, kv{k, v})
}
// 按键降序排序(因为你要的是最大的k个数)
sort.Slice(pairs, func(i, j int) bool {
if pairs[i].Value > pairs[j].Value {
return true
} else if pairs[i].Value < pairs[j].Value {
return false
} else {
if pairs[i].Key > pairs[j].Key {
return true
} else {
return false
}
}
})
// 计算前k个最大的键*值的和
sum := 0
for i := 0; i < len(pairs) && i < x; i++ {
sum += pairs[i].Value * pairs[i].Key
}
return sum
}
得到0的操作数 #
给你两个 非负 整数 num1 和 num2 。
每一步 操作 中,如果 num1 >= num2 ,你必须用 num1 减 num2 ;否则,你必须用 num2 减 num1 。
- 例如,
num1 = 5且num2 = 4,应该用num1减num2,因此,得到num1 = 1和num2 = 4。然而,如果num1 = 4且num2 = 5,一步操作后,得到num1 = 4和num2 = 1。
返回使 num1 = 0 或 num2 = 0 的 操作数 。
示例 1:
输入:num1 = 2, num2 = 3
输出:3
解释:
- 操作 1 :num1 = 2 ,num2 = 3 。由于 num1 < num2 ,num2 减 num1 得到 num1 = 2 ,num2 = 3 - 2 = 1 。
- 操作 2 :num1 = 2 ,num2 = 1 。由于 num1 > num2 ,num1 减 num2 。
- 操作 3 :num1 = 1 ,num2 = 1 。由于 num1 == num2 ,num1 减 num2 。
此时 num1 = 0 ,num2 = 1 。由于 num1 == 0 ,不需要再执行任何操作。
所以总操作数是 3 。
func countOperations(num1 int, num2 int) int {
num:=0
for {
if num1==0||num2==0{
break
}
if num1>=num2{
num1=num1-num2
}else{
num2=num2-num1
}
num++
}
return num
}
使数组和能被K整除的最少操作次数 #
给你一个整数数组 nums 和一个整数 k。你可以执行以下操作任意次:
- 选择一个下标
i,并将nums[i]替换为nums[i] - 1。
返回使数组元素之和能被 k 整除所需的最小操作次数。
示例 1:
输入: nums = [3,9,7], k = 5
输出: 4
解释:
- 对
nums[1] = 9执行 4 次操作。现在nums = [3, 5, 7]。 - 数组之和为 15,可以被 5 整除。
示例 2:
输入: nums = [4,1,3], k = 4
输出: 0
**解释:**数组之和为 8,已经可以被 4 整除。因此不需要操作。
func minOperations(nums []int, k int) int {
var num int
for _,v:=range nums{
num+=v
}
return num%k
}
中等 #
优质数对的总数2 #
给你两个整数数组 nums1 和 nums2,长度分别为 n 和 m。同时给你一个正整数 k。
如果 nums1[i] 可以被 nums2[j] * k 整除,则称数对 (i, j) 为 优质数对(0 <= i <= n - 1, 0 <= j <= m - 1)。
返回 优质数对 的总数。
示例 1:
**输入:**nums1 = [1,3,4], nums2 = [1,3,4], k = 1
**输出:**5
解释:
5个优质数对分别是 (0, 0), (1, 0), (1, 1), (2, 0), 和 (2, 2)。
示例 2:
**输入:**nums1 = [1,2,4,12], nums2 = [2,4], k = 3
**输出:**2
解释:
2个优质数对分别是 (3, 0) 和 (3, 1)。
超出时间限制:
func numberOfPairs(nums1 []int, nums2 []int, k int) int64 {
nums1Data:=make(map[int]int,len(nums1))
nums1MaxNumber:=0
for _,nums:=range nums1{
nums1Data[nums]++
if nums>nums1MaxNumber{
nums1MaxNumber=nums
}
}
var number int64
for _,num2:=range nums2{
for i:=num2*k;i<=nums1MaxNumber;i+=num2*k{
if a,ok:=nums1Data[i];ok{
number+=int64(a)
}
}
}
return number
}
官方:
func numberOfPairs(nums1 []int, nums2 []int, k int) int64 {
count := make(map[int]int)
count2 := make(map[int]int)
max1 := 0
for _, num := range nums1 {
count[num]++
if num > max1 {
max1 = num
}
}
for _, num := range nums2 {
count2[num]++
}
var res int64
for a, cnt := range count2 {
for b := a * k; b <= max1; b += a * k {
if _, ok := count[b]; ok {
res += int64(count[b] * cnt)
}
}
}
return res
}
向字符串添加空格 #
给你一个下标从 0 开始的字符串 s ,以及一个下标从 0 开始的整数数组 spaces 。
数组 spaces 描述原字符串中需要添加空格的下标。每个空格都应该插入到给定索引处的字符值 之前 。
- 例如,
s = "EnjoyYourCoffee"且spaces = [5, 9],那么我们需要在'Y'和'C'之前添加空格,这两个字符分别位于下标5和下标9。因此,最终得到"Enjoy ***Y***our ***C***offee"。
请你添加空格,并返回修改后的字符串*。*
示例 1:
输入:s = "LeetcodeHelpsMeLearn", spaces = [8,13,15]
输出:"Leetcode Helps Me Learn"
解释:
下标 8、13 和 15 对应 "LeetcodeHelpsMeLearn" 中加粗斜体字符。
接着在这些字符前添加空格。
//超出时间限制
func addSpaces(s string, spaces []int) string {
sLen := len(s)
result := ""
for i, v := range spaces {
if v < sLen {
if i == 0 {
result = s[:v]
continue
}
result = result + " " + string(s[spaces[i-1]:spaces[i]])
}
}
result = result + " " + string(s[spaces[len(spaces)-1]:])
return result
}
//超出时间限制
func addSpaces(s string, spaces []int) string {
spacesLen := len(spaces)
j:=0
result := ""
for i, v := range s {
if j<spacesLen&&i==spaces[j]{
result=result+" "+string(v)
j++
}else{
result=result+string(v)
}
}
return result
}
//通过
func addSpaces(s string, spaces []int) string {
var res strings.Builder
ptr := 0
for i ,v:=range s{
if ptr < len(spaces) && i == spaces[ptr] {
res.WriteByte(' ')
ptr++
}
res.WriteRune(v)
}
return res.String()
}
在 Go 中,字符串是不可变的,每次使用 + 拼接字符串都会创建一个新的字符串并复制所有内容。当字符串较大或循环次数较多时,这种操作会带来严重的性能问题。
Go 的 strings.Builder 是专门为高效构建字符串设计的工具,它通过预分配内存和缓冲区复用,避免了频繁的内存分配和复制。
从盒子中找出字典序最大的字符串 I #
给你一个字符串 word 和一个整数 numFriends。
Alice 正在为她的 numFriends 位朋友组织一个游戏。游戏分为多个回合,在每一回合中:
word被分割成numFriends个 非空 字符串,且该分割方式与之前的任意回合所采用的都 不完全相同 。- 所有分割出的字符串都会被放入一个盒子中。
在所有回合结束后,找出盒子中 字典序最大的 字符串。
示例 1:
输入: word = “dbca”, numFriends = 2
输出: “dbc”
解释:
所有可能的分割方式为:
"d"和"bca"。"db"和"ca"。"dbc"和"a"。
你只需要知道计算字符串字典序用 max(a,b)函数
abcdefg 3 7-3+1=5 abcde 从零开始 “”和word[0:5] word[1:6] word[2:7] word[3:7] word[4:7] ... 所以min(i+n-numFriends+1,n)
func answerString(word string, numFriends int) string {
if numFriends==1{
return word
}
n:=len(word)
res:=""
for i:=0;i<n;i++{
res=max(res,word[i:min(i+n-numFriends+1,n)])
}
return res
}
按字典序排列最小的等效字符串 #
给出长度相同的两个字符串s1 和 s2 ,还有一个字符串 baseStr 。
其中 s1[i] 和 s2[i] 是一组等价字符。
- 举个例子,如果
s1 = "abc"且s2 = "cde",那么就有'a' == 'c', 'b' == 'd', 'c' == 'e'。
等价字符遵循任何等价关系的一般规则:
- 自反性 :
'a' == 'a' - 对称性 :
'a' == 'b'则必定有'b' == 'a' - 传递性 :
'a' == 'b'且'b' == 'c'就表明'a' == 'c'
例如, s1 = "abc" 和 s2 = "cde" 的等价信息和之前的例子一样,那么 baseStr = "eed" , "acd" 或 "aab",这三个字符串都是等价的,而 "aab" 是 baseStr 的按字典序最小的等价字符串
利用 s1 和 s2 的等价信息,找出并返回 baseStr 的按字典序排列最小的等价字符串。
示例 1:
输入:s1 = "parker", s2 = "morris", baseStr = "parser"
输出:"makkek"
解释:根据 A 和 B 中的等价信息,我们可以将这些字符分为 [m,p], [a,o], [k,r,s], [e,i] 共 4 组。每组中的字符都是等价的,并按字典序排列。所以答案是 "makkek"。
func smallestEquivalentString(s1 string, s2 string, baseStr string) string {
uf := NewUnionFind(26) //注意这里是26个字母
for i := 0; i < len(s1); i++ {
x := s1[i] - 'a'
y := s2[i] - 'a'
uf.union(int(x), int(y))
}
s := []byte(baseStr)
for i := 0; i < len(baseStr); i++ {
s[i] = byte(uf.find(int(s[i]-'a') )+ 'a') //注意别+错了
}
return string(s)
}
type UnionFind struct {
parent []int
}
func NewUnionFind(n int) *UnionFind {
uf := new(UnionFind)
uf.parent = make([]int, n)
for i := 0; i < n; i++ {
uf.parent[i] = i
}
return uf
}
func (uf *UnionFind) find(x int) int {
if uf.parent[x] != x {
uf.parent[x] = uf.find(uf.parent[x])
}
return uf.parent[x]
}
func (uf *UnionFind) union(x, y int) {
x, y = uf.find(x), uf.find(y) //查找根节点
if x == y { //同一棵树
return
}
if x > y { //// 总是让字典序更小的作为集合代表字符 根据情况,也可以换成最大的或者不换
x, y = y, x
}
uf.parent[y] = x
}
删除星号以后字典序最小的字符串 #
给你一个字符串 s 。它可能包含任意数量的 '*' 字符。你的任务是删除所有的 '*' 字符。
当字符串还存在至少一个 '*' 字符时,你可以执行以下操作:
- 删除最左边的
'*'字符,同时删除该星号字符左边一个字典序 最小 的字符。如果有多个字典序最小的字符,你可以删除它们中的任意一个。
请你返回删除所有 '*' 字符以后,剩余字符连接而成的 字典序最小 的字符串。
示例 1:
**输入:*s = “aaba”
输出:“aab”
解释:
删除 '*' 号和它左边的其中一个 'a' 字符。如果我们选择删除 s[3] ,s 字典序最小。
示例 2:
**输入:**s = “abc”
输出:“abc”
**解释:**字符串中没有 '*' 字符。
根据题意可知,每遇到一个 ‘∗’ 时,则需要去除左侧字典序最小的字符,由于每次要要去掉字典序最小的字母,为了让字典序尽量小,根据贪心原则,相比去掉前面的字符,去掉后面的字符更优,这样才能保证最小的字符尽可能的靠前,使得字符串整体的字典序最小。
我们从左到右遍历字符串 s,由于字符串只包含小写字母,用 26 个栈来保存当前已遍历过的每种字符的索引,第 k 个栈维护第 k 个小写字母的索引。
当遇到字符 ‘∗’ 时,找到非空且字典序最小的栈,在字符串 s 种标记栈顶元素对应的字符为 ‘∗’,并移除栈顶元素;
当遇到非字符 ‘∗’ 时,则将当前索引 i 压入到对应的栈。
最后从左到右选取字符串 s 中不为 ‘∗’ 的字符构成的字符串即为答案。
func clearStars(s string) string {
size := len(s)
cnt := make([][]int, 26)
for i := 0; i < 26; i++ { //建立26个栈,保存当前已遍历过的每种字符的索引
cnt[i] = make([]int, 0)
}
ss := []rune(s)
for i, v := range s {
if v != '*' {
cnt[v-'a'] = append(cnt[v-'a'], i)
} else {
for i := 0; i < 26; i++ {
if len(cnt[i]) > 0 {
n := cnt[i][len(cnt[i])-1] //最小值的最后一个索引
cnt[i]=cnt[i][:len(cnt[i])-1] //栈出一个
ss[n]='*' //删除的空位填充
break
}
}
}
}
sss:=make([]rune, 0)
for i:=0;i<size;i++ { //遍历一遍 去掉*
if ss[i] != '*' {
sss = append(sss, ss[i])
}
}
return string(sss)
}
使用机器人打印字典序最小的字符串 #
给你一个字符串 s 和一个机器人,机器人当前有一个空字符串 t 。执行以下操作之一,直到 s 和 t 都变成空字符串:
- 删除字符串
s的 第一个 字符,并将该字符给机器人。机器人把这个字符添加到t的尾部。 - 删除字符串
t的 最后一个 字符,并将该字符给机器人。机器人将该字符写到纸上。
请你返回纸上能写出的字典序最小的字符串。
示例 1:
输入:s = "zza"
输出:"azz"
解释:用 p 表示写出来的字符串。
一开始,p="" ,s="zza" ,t="" 。
执行第一个操作三次,得到 p="" ,s="" ,t="zza" 。
执行第二个操作三次,得到 p="azz" ,s="" ,t="" 。
示例 2:
输入:s = "bac"
输出:"abc"
解释:用 p 表示写出来的字符串。
执行第一个操作两次,得到 p="" ,s="c" ,t="ba" 。
执行第二个操作两次,得到 p="ab" ,s="c" ,t="" 。
执行第一个操作,得到 p="ab" ,s="" ,t="c" 。
执行第二个操作,得到 p="abc" ,s="" ,t="" 。
示例 3:
输入:s = "bdda"
输出:"addb"
解释:用 p 表示写出来的字符串。
一开始,p="" ,s="bdda" ,t="" 。
执行第一个操作四次,得到 p="" ,s="" ,t="bdda" 。
执行第二个操作四次,得到 p="addb" ,s="" ,t="" 。
提示:
1 <= s.length <= 105s只包含小写英文字母。
方法一:贪心 + 栈
思路
这题其实是给了一个栈的入栈序列,要求出栈序列字典序最小。考虑栈顶元素 c 和字符串 s 中剩余字符中最小的字符 minCharacter:
如果 c<minCharacter,那么要将栈顶元素出栈,才能保证出栈序列最小。 如果 c>minCharacter,那么要将栈顶元素保留,并不停入栈,直到 minCharacter 才能保证出栈序列最小。 如果 c=minCharacter,那么也要将栈顶元素出栈,才能保证出栈序列最小。因为这样做的话,我们可以先将 c 出栈,然后再不停入栈后将 minCharacter 出栈,出栈序列中有两个连续的最小字符。否则如果先不停入栈后将 minCharacter 出栈,我们只能得到一个最小字符,后续的字符只会大于等于该最小字符。 有了这个贪心的思路,我们可以每次将一个字符入栈,然后更新字符串 s 中剩余字符中最小的字符 minCharacter,并不停比较栈顶元素和 minCharacter 的大小,如果符合条件则出栈,否则就进入下一次循环。最后返回结果。
func robotWithString2(s string) string {
cnt := make([]int, 26)
for i := 0; i < len(s); i++ {
cnt[s[i]-'a']++ //先记录所有的字母
}
//创建一个栈
stack := make([]byte, 0)
res := make([]byte, 0)
minCharacter := 0 //比栈顶
for _, v := range s {
stack = append(stack, byte(v)) //先入栈
cnt[v-'a']--
//找出下一个最小字符 用来判断要不要出栈
for j := 0; j < 26; j++ {
if cnt[j] > 0 {
minCharacter = j + 'a'
break
}
}
//出栈 出多少次停止? 栈>0,栈顶元素<=最小字符 一直出到栈顶大于最小字符串
for len(stack) > 0 && stack[len(stack)-1] <= byte(minCharacter) {
//不是出完为止,是出栈顶元素
res = append(res, stack[len(stack)-1])
stack = stack[:len(stack)-1]
}
}
for len(stack) > 0 { //记得最后出栈,出完为止,
res = append(res, stack[len(stack)-1])
stack = stack[:len(stack)-1]
}
return string(res)
}
字典序排数 #
给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。
你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。
示例 1:
输入:n = 13
输出:[1,10,11,12,13,2,3,4,5,6,7,8,9]
示例 2:
输入:n = 2
输出:[1,2]
输入:n = 32
输出:[1,10,11,12,13,14,15,16,17,18,19,2,20,21,22,23,24,25,26,27,28,29,3,30,31,32,4,5,6,7,8,9]
题目要求设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法,因此我们不能使用直接排序的方法。
那么对于一个整数 number,它的下一个字典序整数对应下面的规则:
尝试在 number 后面附加一个零,即 number×10,如果 number×10≤n,那么说明 number×10 是下一个字典序整数;
如果 numbermod10=9 或 number+1>n,那么说明末尾的数位已经搜索完成,退回上一位,即 number=⌊ 10 number ⌋,然后继续判断直到 numbermod10 \ =9 且 number+1≤n 为止,那么 number+1 是下一个字典序整数。
字典序最小的整数为 number=1,我们从它开始,然后依次获取下一个字典序整数,加入结果中,结束条件为已经获取到 n 个整数。
func lexicalOrder(n int) []int {
res:=make([]int,n )
num:=1
for i:=range n{
res[i]=num //第一个传1 注意它在这里
if num*10<=n{
num=num*10 //到10
}else{ //从10 一直到19
for num%10==9|| num+1>n{ //到9了,或者下一个要超了
num=num/10
}
num++
}
}
return res
}
银行中的激光束数量 #
银行内部的防盗安全装置已经激活。给你一个下标从 0 开始的二进制字符串数组 bank ,表示银行的平面图,这是一个大小为 m x n 的二维矩阵。 bank[i] 表示第 i 行的设备分布,由若干 '0' 和若干 '1' 组成。'0' 表示单元格是空的,而 '1' 表示单元格有一个安全设备。
对任意两个安全设备而言,如果****同时 满足下面两个条件,则二者之间存在 一个 激光束:
- 两个设备位于两个 不同行 :
r1和r2,其中r1 < r2。 - 满足
r1 < i < r2的 所有 行i,都 没有安全设备 。
激光束是独立的,也就是说,一个激光束既不会干扰另一个激光束,也不会与另一个激光束合并成一束。
返回银行中激光束的总数量。
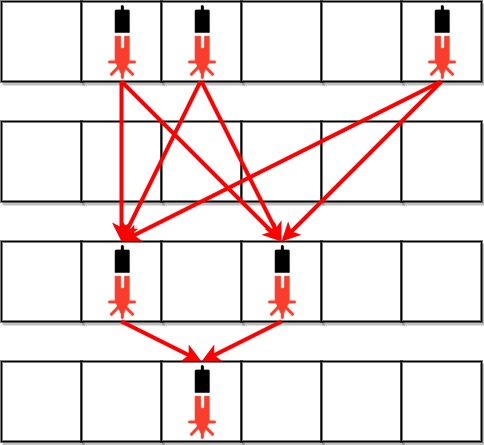
输入:bank = ["011001","000000","010100","001000"]
输出:8
解释:在下面每组设备对之间,存在一条激光束。总共是 8 条激光束:
* bank[0][1] -- bank[2][1]
* bank[0][1] -- bank[2][3]
* bank[0][2] -- bank[2][1]
* bank[0][2] -- bank[2][3]
* bank[0][5] -- bank[2][1]
* bank[0][5] -- bank[2][3]
* bank[2][1] -- bank[3][2]
* bank[2][3] -- bank[3][2]
注意,第 0 行和第 3 行上的设备之间不存在激光束。
这是因为第 2 行存在安全设备,这不满足第 2 个条件。
func numberOfBeams(bank []string) int {
allNum := 0
firstL := false
firstNum, secondNum := 0, 0
for i := 0; i < len(bank); i++ {
n := len(bank[i])
for j := 0; j < n; j++ {
if bank[i][j] == '1' {
if !firstL {
firstNum++
} else {
secondNum++
allNum += firstNum
}
}
}
if firstNum > 0 {
firstL = true
}
if secondNum > 0 {
firstNum = secondNum
secondNum = 0
}
}
return allNum
}
func numberOfBeams(bank []string) int {
last, ans := 0, 0
for _, line := range bank {
cnt := strings.Count(line, "1")
if cnt != 0 {
ans += last * cnt
last = cnt
}
}
return ans
}
从链表中移除在数组中存在的节点 #
给你一个整数数组 nums 和一个链表的头节点 head。从链表中移除所有存在于 nums 中的节点后,返回修改后的链表的头节点。
示例 1:
输入: nums = [1,2,3], head = [1,2,3,4,5]
输出: [4,5]
解释:

移除数值为 1, 2 和 3 的节点。
示例 2:
输入: nums = [1], head = [1,2,1,2,1,2]
输出: [2,2,2]
解释:

移除数值为 1 的节点。
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func modifiedList(nums []int, head *ListNode) *ListNode {
exist:=make(map[int]struct{})
for _,v:=range nums{
exist[v]=struct{}{}
}
q:=&ListNode{-1,head}
head=q
for q.Next!=nil{
if _,ok:=exist[q.Next.Val];ok{
q.Next=q.Next.Next
}else{
q=q.Next
}
}
return head.Next
}
统计网格图中没有被保卫的格子数 #
给你两个整数 m 和 n 表示一个下标从 0 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和 walls ,其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ,分别表示第 i 个警卫和第 j 座墙所在的位置。
一个警卫能看到 4 个坐标轴方向(即东、南、西、北)的 所有 格子,除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到,那么我们说这个格子被 保卫 了。
请你返回空格子中,有多少个格子是 没被保卫 的。
示例 1:
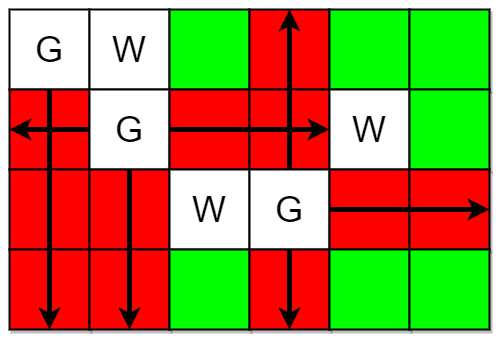
输入:m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
输出:7
解释:上图中,被保卫和没有被保卫的格子分别用红色和绿色表示。
总共有 7 个没有被保卫的格子,所以我们返回 7 。
func countUnguarded(m int, n int, guards [][]int, walls [][]int) int {
field := make([][]int, 0)
for i := 0; i < m; i++ {
field = append(field, make([]int, n))
}
for i := 0; i < len(guards); i++ {
field[guards[i][0]][guards[i][1]] = 1
}
for i := 0; i < len(walls); i++ {
field[walls[i][0]][walls[i][1]] = 2
}
for i := 0; i < m; i++ { //改成3
for j := 0; j < n; j++ {
if field[i][j] == 1 {
field = countGuard(i, j, field)
}
}
}
count := 0
for i := 0; i < m; i++ { //最后再统计一遍
for j := 0; j < n; j++ {
if field[i][j] == 0 {
count++
}
}
}
return count
}
func countGuard(m int, n int, field [][]int) [][]int {
for i, j := m, n-1; j >= 0; j-- { //左
if field[i][j] == 1 || field[i][j] == 2 {
break
}
field[i][j] = 3
}
for i, j := m, n+1; j < len(field[0]); j++ { //右
if field[i][j] == 1 || field[i][j] == 2 {
break
}
field[i][j] = 3
}
for i, j := m-1, n; i >= 0; i-- { //上
if field[i][j] == 1 || field[i][j] == 2 {
break
}
field[i][j] = 3
}
for i, j := m+1, n; i < len(field); i++ { //下
if field[i][j] == 1 || field[i][j] == 2 {
break
}
field[i][j] = 3
}
return field
}
使绳子变成彩色的最短 时间 #
Alice 把 n 个气球排列在一根绳子上。给你一个下标从 0 开始的字符串 colors ,其中 colors[i] 是第 i 个气球的颜色。
Alice 想要把绳子装扮成 五颜六色的 ,且她不希望两个连续的气球涂着相同的颜色,所以她喊来 Bob 帮忙。Bob 可以从绳子上移除一些气球使绳子变成 彩色 。给你一个 下标从 0 开始 的整数数组 neededTime ,其中 neededTime[i] 是 Bob 从绳子上移除第 i 个气球需要的时间(以秒为单位)。
返回 Bob 使绳子变成 彩色 需要的 最少时间 。
示例 1:
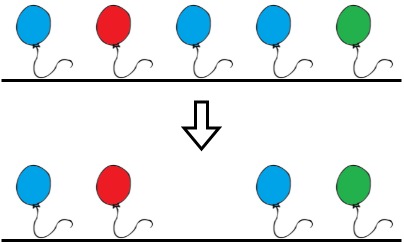
输入:colors = "abaac", neededTime = [1,2,3,4,5]
输出:3
解释:在上图中,'a' 是蓝色,'b' 是红色且 'c' 是绿色。
Bob 可以移除下标 2 的蓝色气球。这将花费 3 秒。
移除后,不存在两个连续的气球涂着相同的颜色。总时间 = 3 。
示例 2:
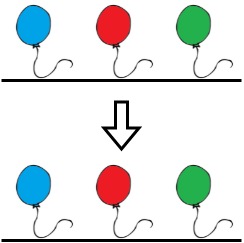
输入:colors = "abc", neededTime = [1,2,3]
输出:0
解释:绳子已经是彩色的,Bob 不需要从绳子上移除任何气球。
func minCost(colors string, neededTime []int) int {
pre := 0 //前一个下标
num := 0
for i := 1; i < len(colors); i++ {
if rune(colors[pre]) == rune(colors[i]) { //相等
if neededTime[pre] < neededTime[i] { //前一个小于当前
num += neededTime[pre] //加上前一个值,同时下标等于当前
pre = i
} else { //当前小
num += neededTime[i] //前一个下标不变
}
} else { //不同 下标转当前
pre = i
}
}
return num
}
电网维护 #
给你一个整数 c,表示 c 个电站,每个电站有一个唯一标识符 id,从 1 到 c 编号。
这些电站通过 n 条 双向 电缆互相连接,表示为一个二维数组 connections,其中每个元素 connections[i] = [ui, vi] 表示电站 ui 和电站 vi 之间的连接。直接或间接连接的电站组成了一个 电网 。
最初,所有 电站均处于在线(正常运行)状态。
另给你一个二维数组 queries,其中每个查询属于以下 两种类型之一 :
[1, x]:请求对电站x进行维护检查。如果电站x在线,则它自行解决检查。如果电站x已离线,则检查由与x同一 电网 中 编号最小 的在线电站解决。如果该电网中 不存在 任何 在线 电站,则返回 -1。[2, x]:电站x离线(即变为非运行状态)。
返回一个整数数组,表示按照查询中出现的顺序,所有类型为 [1, x] 的查询结果。
**注意:**电网的结构是固定的;离线(非运行)的节点仍然属于其所在的电网,且离线操作不会改变电网的连接性。
示例 1:
输入: c = 5, connections = [[1,2],[2,3],[3,4],[4,5]], queries = [[1,3],[2,1],[1,1],[2,2],[1,2]]
输出: [3,2,3]
解释:

- 最初,所有电站
{1, 2, 3, 4, 5}都在线,并组成一个电网。 - 查询
[1,3]:电站 3 在线,因此维护检查由电站 3 自行解决。 - 查询
[2,1]:电站 1 离线。剩余在线电站为{2, 3, 4, 5}。 - 查询
[1,1]:电站 1 离线,因此检查由电网中编号最小的在线电站解决,即电站 2。 - 查询
[2,2]:电站 2 离线。剩余在线电站为{3, 4, 5}。 - 查询
[1,2]:电站 2 离线,因此检查由电网中编号最小的在线电站解决,即电站 3。
示例 2:
输入: c = 3, connections = [], queries = [[1,1],[2,1],[1,1]]
输出: [1,-1]
解释:
- 没有连接,因此每个电站是一个独立的电网。
- 查询
[1,1]:电站 1 在线,且属于其独立电网,因此维护检查由电站 1 自行解决。 - 查询
[2,1]:电站 1 离线。 - 查询
[1,1]:电站 1 离线,且其电网中没有其他电站,因此结果为 -1。
将所有元素变为0的最少操作次数 #
给你一个大小为 n 的 非负 整数数组 nums 。你的任务是对该数组执行若干次(可能为 0 次)操作,使得 所有 元素都变为 0。
在一次操作中,你可以选择一个子数组 [i, j](其中 0 <= i <= j < n),将该子数组中所有 最小的非负整数 的设为 0。
返回使整个数组变为 0 所需的最少操作次数。
一个 子数组 是数组中的一段连续元素。
示例 1:
输入: nums = [0,2]
输出: 1
解释:
- 选择子数组
[1,1](即[2]),其中最小的非负整数是 2。将所有 2 设为 0,结果为[0,0]。 - 因此,所需的最少操作次数为 1。
示例 2:
输入: nums = [3,1,2,1]
输出: 3
解释:
- 选择子数组
[1,3](即[1,2,1]),最小非负整数是 1。将所有 1 设为 0,结果为[3,0,2,0]。 - 选择子数组
[2,2](即[2]),将 2 设为 0,结果为[3,0,0,0]。 - 选择子数组
[0,0](即[3]),将 3 设为 0,结果为[0,0,0,0]。 - 因此,最少操作次数为 3。
func minOperations(nums []int) int {
st:=make([]int,0)
num:=0
for _,v:=range nums{ //下面操作顺序不能乱
for len(st)>0 && st[len(st)-1]>v{ //出栈
st=st[:len(st)-1]
}
if v==0{
continue
}
if len(st)==0||st[len(st)-1]<v{ //入栈
num++
st=append(st,v)
}
}
return num
}
一和零 #
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
//动态规划
// 其中 dp[i][j][k] 表示在前 i 个字符串中,使用 j 个 0 和 k 个 1 的情况下最多可以得到的字符串数量。
func findMaxForm(strs []string, m int, n int) int {
lenS := len(strs)
dp := make([][][]int, lenS+1)
for i, _ := range dp {
dp[i] = make([][]int, m+1)
for j, _ := range dp[i] {
dp[i][j] = make([]int, n+1)
}
}
for i := 1; i <= lenS; i++ {
zeros := strings.Count(strs[i-1], "0") //前一个字符串0的数量
ones := len(strs[i-1]) - zeros //前一个字符串1的数量
for j := 0; j <= m; j++ {
for k := 0; k <= n; k++ {
dp[i][j][k] = dp[i-1][j][k] //前i个字符串中,使用j 个 0 和 k 个 1 的情况可以得到的字符串数量先等于 前i-1个字符串中
if j >= zeros && k >= ones { //越界了
dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-zeros][k-ones]+1) //前i-1个字符串中j 个 0 和 k 个 1 的数量,
// 与前i-1个字符串中j-zeros个0,k-ones1的数量大最大值
}
}
}
}
return dp[lenS][m][n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
将1移动到末尾的最大操作数 #
给你一个 二进制字符串 s。
你可以对这个字符串执行 任意次 下述操作:
- 选择字符串中的任一下标
i(i + 1 < s.length),该下标满足s[i] == '1'且s[i + 1] == '0'。 - 将字符
s[i]向 右移 直到它到达字符串的末端或另一个'1'。例如,对于s = "010010",如果我们选择i = 1,结果字符串将会是s = "0**001**10"。
返回你能执行的 最大 操作次数。
示例 1:
输入: s = “1001101”
输出: 4
解释:
可以执行以下操作:
- 选择下标
i = 0。结果字符串为s = "**001**1101"。 - 选择下标
i = 4。结果字符串为s = "0011**01**1"。 - 选择下标
i = 3。结果字符串为s = "001**01**11"。 - 选择下标
i = 2。结果字符串为s = "00**01**111"。
//110
func maxOperations(s string) int {
count := 0
oneCount := 0
preZero := false
for i := 0; i < len(s); i++ {
if s[i] == byte('1') {
if preZero {
count += oneCount
preZero = false
}
oneCount++
} else {
preZero = true
if i+1 == len(s) { //解决110 问题
count += oneCount
}
}
}
return count
}
仅含1的子串数 #
给你一个二进制字符串 s(仅由 ‘0’ 和 ‘1’ 组成的字符串)。
返回所有字符都为 1 的子字符串的数目。
由于答案可能很大,请你将它对 10^9 + 7 取模后返回。
示例 1:
输入:s = "0110111"
输出:9
解释:共有 9 个子字符串仅由 '1' 组成
"1" -> 5 次
"11" -> 3 次
"111" -> 1 次
func numSub(s string) int {
ss := []byte(s)
sub := 0
i, j := 0, 0
for ; j < len(ss); j++ {
if s[j] == byte('0') {
if i != j {
sub += getSunb(j - i)
}
i = j + 1
}
}
sub += getSunb(j - i)
return sub % (int(math.Pow(float64(10), float64(9))) + 7)
}
func getSunb(s int) int {
return s * (s + 1) / 2
}
简易银行系统 #
你的任务是为一个很受欢迎的银行设计一款程序,以自动化执行所有传入的交易(转账,存款和取款)。银行共有 n 个账户,编号从 1 到 n 。每个账号的初始余额存储在一个下标从 0 开始的整数数组 balance 中,其中第 (i + 1) 个账户的初始余额是 balance[i] 。
请你执行所有 有效的 交易。如果满足下面全部条件,则交易 有效 :
- 指定的账户编号在
1和n之间,且 - 取款或者转账需要的钱的总数 小于或者等于 账户余额。
实现 Bank 类:
Bank(long[] balance)使用下标从 0 开始的整数数组balance初始化该对象。boolean transfer(int account1, int account2, long money)从编号为account1的账户向编号为account2的账户转帐money美元。如果交易成功,返回true,否则,返回false。boolean deposit(int account, long money)向编号为account的账户存款money美元。如果交易成功,返回true;否则,返回false。boolean withdraw(int account, long money)从编号为account的账户取款money美元。如果交易成功,返回true;否则,返回false。
示例:
输入:
["Bank", "withdraw", "transfer", "deposit", "transfer", "withdraw"]
[[[10, 100, 20, 50, 30]], [3, 10], [5, 1, 20], [5, 20], [3, 4, 15], [10, 50]]
输出:
[null, true, true, true, false, false]
解释:
Bank bank = new Bank([10, 100, 20, 50, 30]);
bank.withdraw(3, 10); // 返回 true ,账户 3 的余额是 $20 ,所以可以取款 $10 。
// 账户 3 余额为 $20 - $10 = $10 。
bank.transfer(5, 1, 20); // 返回 true ,账户 5 的余额是 $30 ,所以可以转账 $20 。
// 账户 5 的余额为 $30 - $20 = $10 ,账户 1 的余额为 $10 + $20 = $30 。
bank.deposit(5, 20); // 返回 true ,可以向账户 5 存款 $20 。
// 账户 5 的余额为 $10 + $20 = $30 。
bank.transfer(3, 4, 15); // 返回 false ,账户 3 的当前余额是 $10 。
// 所以无法转账 $15 。
bank.withdraw(10, 50); // 返回 false ,交易无效,因为账户 10 并不存在。
type Bank []int64
func Constructor(balance []int64) Bank {
return balance
}
func (b Bank) Transfer(account1, account2 int, money int64) bool {
if account1 > len(b) || account2 > len(b) || b[account1-1] < money {
return false
}
b[account1-1] -= money
b[account2-1] += money
return true
}
func (b Bank) Deposit(account int, money int64) bool {
if account > len(b) {
return false
}
b[account-1] += money
return true
}
func (b Bank) Withdraw(account int, money int64) bool {
if account > len(b) || b[account-1] < money {
return false
}
b[account-1] -= money
return true
}
长度可以被K整除的子数组的最大元素和 #
给你一个整数数组 nums 和一个整数 k 。
返回 nums 中一个 非空子数组 的 最大 和,要求该子数组的长度可以 被 k 整除。
示例 1:
输入: nums = [1,2], k = 1
输出: 3
**解释:**子数组 [1, 2] 的和为 3,其长度为 2,可以被 1 整除。
示例 2:
输入: nums = [-1,-2,-3,-4,-5], k = 4
输出: -10
**解释:**满足题意且和最大的子数组是 [-1, -2, -3, -4],其长度为 4,可以被 4 整除。
示例 3:
输入: nums = [-5,1,2,-3,4], k = 2
输出: 4
**解释:**满足题意且和最大的子数组是 [1, 2, -3, 4],其长度为 4,可以被 2 整除。
困难 #
公司命名 #
给你一个字符串数组 ideas 表示在公司命名过程中使用的名字列表。公司命名流程如下:
- 从
ideas中选择 2 个 不同 名字,称为ideaA和ideaB。 - 交换
ideaA和ideaB的首字母。 - 如果得到的两个新名字 都 不在
ideas中,那么ideaA ideaB(串联ideaA和ideaB,中间用一个空格分隔)是一个有效的公司名字。 - 否则,不是一个有效的名字。
返回 不同 且有效的公司名字的数目。
示例 1:
输入:ideas = ["coffee","donuts","time","toffee"]
输出:6
解释:下面列出一些有效的选择方案:
- ("coffee", "donuts"):对应的公司名字是 "doffee conuts" 。
- ("donuts", "coffee"):对应的公司名字是 "conuts doffee" 。
- ("donuts", "time"):对应的公司名字是 "tonuts dime" 。
- ("donuts", "toffee"):对应的公司名字是 "tonuts doffee" 。
- ("time", "donuts"):对应的公司名字是 "dime tonuts" 。
- ("toffee", "donuts"):对应的公司名字是 "doffee tonuts" 。
因此,总共有 6 个不同的公司名字。
下面列出一些无效的选择方案:
- ("coffee", "time"):在原数组中存在交换后形成的名字 "toffee" 。
- ("time", "toffee"):在原数组中存在交换后形成的两个名字。
- ("coffee", "toffee"):在原数组中存在交换后形成的两个名字。
示例 2:
输入:ideas = ["lack","back"]
输出:0
解释:不存在有效的选择方案。因此,返回 0 。
提示:
2 <= ideas.length <= 5 * 1041 <= ideas[i].length <= 10ideas[i]由小写英文字母组成ideas中的所有字符串 互不相同
超时结果:
func distinctNames(ideas []string) int64 {
list := make(map[string]struct{}, 0)
for _, idea := range ideas {
list[idea] = struct{}{}
}
var number int64 = 0
for i := 0; i < len(ideas); i++ {
for j := i + 1; j < len(ideas); j++ {
i_idea, j_idea := []byte(ideas[i]), []byte(ideas[j])
if i_idea[0] == j_idea[0] {
continue
} else {
a := i_idea[0]
i_idea[0] = j_idea[0]
j_idea[0] = a
if _, ok := list[string(i_idea)]; ok {
continue
}
if _, ok := list[string(j_idea)]; ok {
continue
}
number += 2
}
}
}
return number
}
字典序的第K小数字 #
给定整数 n 和 k,返回 [1, n] 中字典序第 k 小的数字。
示例 1:
输入: n = 13, k = 2
输出: 10
解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第二小的数字是 10。
示例 2:
输入: n = 1, k = 1
输出: 1
//超时结果:
func findKthNumber(n int, k int) int {
v:=1
j:=0
for i:=0;i<n;i++{
j++
if j==k{
break
}
if v*10<=n{
v=v*10
}else{
for v+1>n||v%10==9{
v=v/10
}
v++
}
}
return v
}
形成目标数组的子数组最少增加次数 #
给你一个整数数组 target 和一个数组 initial ,initial 数组与 target 数组有同样的维度,且一开始全部为 0 。
请你返回从 initial 得到 target 的最少操作次数,每次操作需遵循以下规则:
- 在
initial中选择 任意 子数组,并将子数组中每个元素增加 1 。
答案保证在 32 位有符号整数以内。
示例 1:
输入:target = [1,2,3,2,1]
输出:3
解释:我们需要至少 3 次操作从 intial 数组得到 target 数组。
[0,0,0,0,0] 将下标为 0 到 4 的元素(包含二者)加 1 。
[1,1,1,1,1] 将下标为 1 到 3 的元素(包含二者)加 1 。
[1,2,2,2,1] 将下表为 2 的元素增加 1 。
[1,2,3,2,1] 得到了目标数组。
示例 2:
输入:target = [3,1,1,2]
输出:4
解释:(initial)[0,0,0,0] -> [1,1,1,1] -> [1,1,1,2] -> [2,1,1,2] -> [3,1,1,2] (target) 。
示例 3:
输入:target = [3,1,5,4,2]
输出:7
解释:(initial)[0,0,0,0,0] -> [1,1,1,1,1] -> [2,1,1,1,1] -> [3,1,1,1,1]
-> [3,1,
//超时了
func minNumberOperations(target []int) int {
if len(target) == 1 {
return target[0]
}
for i := 0; i < len(target); i++ {
if target[i] == 0 {
if i == 0 {
if i+1 < len(target) {
return minNumberOperations(target[i+1:])
} else {
return 0
}
} else {
if i+1 < len(target) {
return minNumberOperations(target[:i]) + minNumberOperations(target[i+1:]) + 1
} else {
return minNumberOperations(target[:i]) + 1
}
}
} else {
n := target[i]
target[i] = n - 1
}
}
return minNumberOperations(target) + 1
}
3 1 5 4 2
如果 target[i]≥target[i+1],那么在给 target[i] 增加 1 时,可以顺便给 target[i+1] 增加 1,这样 target[i+1] 不会占用额外的操作次数;
如果 target[i]<target[i+1],那么即使在给 target[i] 增加 1 的同时顺便给 target[i+1] 增加 1,那么还需要 target[i+1]−target[i] 次操作才能得到正确的结果。
func minNumberOperations2(target []int) int {
n := len(target)
ans := target[0]
for i := 1; i < n; i++ {
ans += max(target[i]-target[i-1], 0)
}
return ans
}