通过椭圆曲线加密实现数字签名 #
私钥公钥如何产生? #
随机生成一个256位的二进制数
11011100111110101100101010000100111100101000011…………………
dcfaca84f325f65a…,…………… 16进制
一、为什么叫椭圆曲线 #
圆锥曲线可以用二次方程表示。椭圆曲线是用三次方程表示,如下:
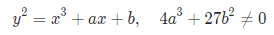 其中,a 和 b 的取值不同,椭圆曲线的形状会有所改变,经典的形状如下图所示:
其中,a 和 b 的取值不同,椭圆曲线的形状会有所改变,经典的形状如下图所示:

椭圆曲线有以下两个特点:
- 画一条直线跟椭圆曲线相交,它们最多有三个交点;
- 关于 X 轴对称。
A(x,y) k* A
二、椭圆曲线运算法则 #
1. 椭圆曲线加法 #
根据上面介绍的椭圆曲线的特性“画一条直线跟椭圆曲线相交,它们最多有三个交点”,可以进行以下定义:
-
假设椭圆曲线上有 P、Q 两个点,经过这两个点做一条直线和椭圆曲线相交于第三点 R,然后做关于 x 轴的对称点 -R,-R 即是 R 的逆元,根据阿贝尔群的定义,-R 也一定在椭圆曲线上。定义 P+Q = -R,也就是说椭圆曲线上任意两点的和也在椭圆曲线上,同样可以引申出椭圆曲线上任意三点的和为 0 即 P+Q+R = 0。如图:

-
假如 P=Q,则作椭圆曲线在 P 点的切线,与曲线相交于 R,则 R = P+P = 2P

2. 椭圆曲线乘法 #
根据上面椭圆曲线的加法可以得出下列等式:P+P = 2P(过点 P 切线作一条直线)P+2P = 3P(过点 P 和 2P 作一条直线)P+3P = 4P(过点 P 和 3P 作一条直线)假设 P 是椭圆曲线上的一个点,正整数 K 乘以 P 可以总结成公式为:(k-1) * P + P = k * P如果把 k 看作是两个数相乘即 k = m * n,则可以得出满足以下性质(在椭圆曲线密钥交换中会用到):(m * n) * P = m * (n * P) = (n * m)p = n * (m*P)
s * P =K (公钥)
三、椭圆曲线的难题 #
定义在质数阶的有限域上
满足下面公式的曲线,其中 p 是质数,x、y、a、b 都是小于 p 的非负整数:y^2 = x^3 + ax + b (mod p) { (4a^3 + 27b^2!)=0 }
来看一下 y^2 = x^3 - x 这个公式取模后的的图像(p=71):

可以看出,虽然很散乱,但是仔细看这些点都是关于一条直线对称的,这条直线就是 y=71/2 这条水平直线,并且原来椭圆曲线上定义的加法和乘法都可用。
假如选择一个点 P(4,8) 为基点,按照椭圆曲线的加法去运算 2P、3P… 这样的话,最后得到一个 k 次加法后的结果 kP(44,44),请问 k 是多少?
这时看一下上面的散点图,找到 (4,8) 和(44,44)这两个点,很难找出来通过几次椭圆曲线加法转变过去的,更何况这个是在公式中取模的那个质数等于 71 的情况下,如果把这个质数取得很大,难度就更大了,比特币中使用的 Secp256k1 这条曲线中取模的质数 p 等于:
p = 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1
这样一个数,要逐一算出可能性取匹配几乎是不可能的。
G(79BE667E F9DCBBAC………………………………………..)16进制
总结一下椭圆曲线的数学依据:
K = kG
- G 为椭圆曲线上的一个点,叫基点;
- k 为正整数;
- 如果给定小 k 和 G,通过椭圆曲线加法法则去计算 K 很容易;
- 如果给定 K 和 G,求小 k 就非常困难。
一般规定大 K 为公开密钥,小 k 为私钥
公钥P=K * G
非对称加密 #
“非对称加密也叫公钥密码: 使用公钥加密, 使用私钥解密”
数据加密 #
A:
B:
数字签名 #
数字签名是一种将相当于现实世界中的盖章、签字的功能在计算机世界中进行实现的技术。使用数字签名可以识别篡改和伪装,还可以防止否认。
通过数字签名解决问题 #
M 对M进行签名
M X K = N 签名数据
M X P =M X K X G 验证签名
四、 非对称加密和数字签名 #
对称加密与数字签名之间的关系。
非对称加密包括一个由公钥和私钥组成的密钥对,其中公钥用于加密,私钥用于解密。

数字签名中也同样会使用公钥和私钥组成的密钥对,不过这两个密钥的用法和非对称加密是相反的,即用私钥加密相当于生成签名,而用公钥解密则相当于验证签名。

那么为什么加密相当于生成签名,而解密相当于验证签名呢?
用公钥加密所得到的密文,只能用与该公钥配对的私钥才能解密:同样地,用私钥加密所得到的密文,也只能用与该私钥配对的公钥才能解密。也就是说,如果用某个公钥成功解密了密文,那么就能够证明这段密文是用与该公钥配对的私钥进行加密所得到的。
用私钥进行加密这一行为只能由持有私钥的人完成,正是基于这一事实,我们才可以将用私钥加密的密文作为签名来对待。
由于公钥是对外公开的,因此任何人都能够用公钥进行解密,这就产生了一个很大的好处,即任何人都能够对签名进行验证。

数字签名的方法 #
下面我们来具体介绍两种生成和验证数字签名的方法。
- 直接对消息签名的方法
- 对消息的散列值签名的方法
直接对消息签名的方法比较容易理解,但实际上并不会使用;对消息的散列值签名的方法稍微复杂一点,但实际中我们一般都使用这种方法。
使用直接对消息签名的方法,需要对整个消息进行加密,非常耗时,这是因为非对称加密算法本来就非常慢。那么,我们能不能生成一条很短的数据来代替消息本身呢?这就是单向散列函数。
于是我们不必再对整个消息进行加密(即对消息签名),而是只要先用单向散列函数求出消息的散列值,然后再将散列值进行加密(对散列值签名)就可以了。无论消息有多长,散列值永远都是这么短,因此对其进行加密(签名)是非常轻松的。
(1)A用单向散列函数计算消息的散列值。
(2)A用自己的私钥对散列值进行加密。
用私钥加密散列值所得到的密文就是A对这条散列值的签名,由于只有A才持有自己的私钥因此, 除了A以外,其他人是无法生成相同的签名(密文)的。(3)A将消息和签名发送给B。
(4)B用A的公钥对收到的签名进行解密。
如果收到的签名确实是用A的私钥进行加密而得到的密文(签名),那么用A的公钥应该能够正确 解密,解密的结果应该等于消息的散列值。如果收到的签名不是用A的私钥进行加密而得到的密文, 那么就无法用A的公钥正确解密(解密后得到的数据看起来是随机的)。(5)B将签名解密后得到的散列值与A直接发送的消息的散列值进行对比。
如果两者一致,则签名验证成功;如果两者不一致,则签名验证失败。我们将数字签名中生成签名和验证签名的过程整理成一张时间流程图 。
五 使用椭圆曲线进行数字签名 #
椭圆曲线在go中对应的包: import “crypto/elliptic”
使用椭圆曲线在go中进行数字签名: import “crypto/ecdsa”
美国FIPS186-2标准, 推荐使用5个素域上的椭圆曲线, 这5个素数模分别是:
P~192~ = 2^192^ - 2^64^ - 1
P~224~ = 2^224^ - 2^96^ + 1
P~256~ = 2^256^ - 2^224^ + 2^192^ - 2^96^ -1
P~384~ = 2^384^ - 2^128^ - 2^96^ + 2^32^ -1
P~512~ = 2^512^ - 1
-
秘钥对称的生成, 并保存到磁盘
-
使用ecdsa生成密钥对
func GenerateKey(c elliptic.Curve, rand io.Reader) (priv *PrivateKey, err error) -
将私钥写入磁盘
-
使用x509进行序列化
func MarshalECPrivateKey(key *ecdsa.PrivateKey) ([]byte, error) -
将得到的切片字符串放入pem.Block结构体中
block := pem.Block{
Type : “描述….”,
Bytes : MarshalECPrivateKey返回值中的切片字符串,
}
-
使用pem编码
pem.Encode();
-
-
将公钥写入磁盘
-
从私钥中得到公钥
-
使用x509进行序列化
func MarshalPKIXPublicKey(pub interface{}) ([]byte, error) -
将得到的切片字符串放入pem.Block结构体中
block := pem.Block{
Type : “描述….”,
Bytes : MarshalECPrivateKey返回值中的切片字符串,
}
-
使用pem编码
pem.Encode();
-
-
-
使用私钥进行数字签名
-
打开私钥文件, 将内容读出来 ->[]byte
-
使用pem进行数据解码 -> pem.Decode()
-
使用x509, 对私钥进行还原
func ParseECPrivateKey(der []byte) (key *ecdsa.PrivateKey, err error) -
对原始数据进行哈希运算 -> 散列值
-
进行数字签名
func Sign(rand io.Reader, priv *PrivateKey, hash []byte) (r, s *big.Int, err error) - 得到的r和s不能直接使用, 因为这是指针 应该将这两块内存中的数据进行序列化 -> []byte func (z *Int) MarshalText() (text []byte, err error)
-
-
使用公钥验证数字签名
-
打开公钥文件, 将里边的内容读出 -> []byte
-
pem解码 -> pem.Decode()
-
使用x509对公钥还原
func ParsePKIXPublicKey(derBytes []byte) (pub interface{}, err error) -
将接口 -> 公钥
-
对原始数据进行哈希运算 -> 得到散列值
-
签名的认证 - > ecdsa
func Verify(pub *PublicKey, hash []byte, r, s *big.Int) bool - 参数1: 公钥 - 参数2: 原始数据生成的散列值 - 参数3,4: 通过签名得到的连个点 func (z *Int) UnmarshalText(text []byte) error
-
六、Go语言使用椭圆曲线签名认证实现 #
package main
import (
"crypto/ecdsa"
"crypto/elliptic"
"crypto/rand"
"crypto/sha1"
"crypto/x509"
"encoding/pem"
"fmt"
"math/big"
"os"
)
func main() {
GenerateEccKey()
src := []byte("使用x509对pem.Block中的Bytes变量中的数据进行解析 -> 得到一接口")
rText, sText := EccSignature(src, "eccPrivate.pem")
bl := EccVerify(src, rText, sText, "eccPublic.pem")
fmt.Println(bl)
}
// 1. 生成密钥对
func GenerateEccKey() {
//1. 使用ecdsa生成密钥对
privateKey, err := ecdsa.GenerateKey(elliptic.P521(), rand.Reader)
if err != nil {
panic(err)
}
//2. 将私钥写入磁盘
//- 使用x509进行序列化
derText, err := x509.MarshalECPrivateKey(privateKey)
if err != nil {
panic(err)
} //返回私钥
//- 将得到的切片字符串放入pem.Block结构体中
block := pem.Block{
Type : "ecdsa private key",
Bytes : derText,
}
//- 使用pem编码
file, err := os.Create("eccPrivate.pem")
if err != nil {
panic(err)
}
pem.Encode(file, &block)
file.Close()
//3. 将公钥写入磁盘
//- 从私钥中得到公钥
publicKey := privateKey.PublicKey
//- 使用x509进行序列化
derText, err = x509.MarshalPKIXPublicKey(&publicKey)
if err != nil {
panic(err)
}
//- 将得到的切片字符串放入pem.Block结构体中
block = pem.Block{
Type : "ecdsa public key",
Bytes : derText,
}
//- 使用pem编码
file, err = os.Create("eccPublic.pem")
if err != nil {
panic(err)
}
pem.Encode(file, &block)
file.Close()
}
// ecc签名 - 私钥
func EccSignature(plainText []byte, privName string) (rText, sText []byte){
//1. 打开私钥文件, 将内容读出来 ->[]byte
file, err := os.Open(privName)
if err != nil {
panic(err)
}
info, err := file.Stat()
if err != nil {
panic(err)
}
buf := make([]byte, info.Size())
file.Read(buf)
file.Close()
//2. 使用pem进行数据解码 -> pem.Decode()
block, _ := pem.Decode(buf)
//3. 使用x509, 对私钥进行还原
privateKey, err := x509.ParseECPrivateKey(block.Bytes)
if err != nil {
panic(err)
}
//4. 对原始数据进行哈希运算 -> 散列值
hashText := sha1.Sum(plainText)
//5. 进行数字签名
r, s, err := ecdsa.Sign(rand.Reader, privateKey, hashText[:])
if err != nil {
panic(err)
}
// 6. 对r, s内存中的数据进行格式化 -> []byte
rText, err = r.MarshalText()
if err != nil {
panic(err)
}
sText, err = s.MarshalText()
if err != nil {
panic(err)
}
return
}
// ecc签名认证
func EccVerify(plainText, rText, sText []byte, pubFile string) bool {
//1. 打开公钥文件, 将里边的内容读出 -> []byte
file, err := os.Open(pubFile)
if err != nil {
panic(err)
}
info, err := file.Stat()
if err != nil {
panic(err)
}
buf := make([]byte, info.Size())
file.Read(buf)
file.Close()
//2. pem解码 -> pem.Decode()
block, _ := pem.Decode(buf)
//3. 使用x509对公钥还原
pubInterface, err := x509.ParsePKIXPublicKey(block.Bytes)
if err != nil {
panic(err)
}
//4. 将接口 -> 公钥
publicKey := pubInterface.(*ecdsa.PublicKey)
//5. 对原始数据进行哈希运算 -> 得到散列值
hashText := sha1.Sum(plainText)
// 将rText, sText -> int数据
var r, s big.Int
r.UnmarshalText(rText)
s.UnmarshalText(sText)
//6. 签名的认证 - > ecdsa (问题,api的设计为什么在这个地方要传地址,直接传值比较不是更好吗?)
bl := ecdsa.Verify(publicKey, hashText[:], &r, &s)
return bl
}
RSA加密操作 #
func main() {
//加密
src := []byte("少壮不努力,活该你单身,223333")
fmt.Println(string(src))
date, err := EnRsaPublic("/Users/tianzhiwei/go/src/webapp/PublicKey.pem", src)
if err != nil {
panic(err)
}
fmt.Println("非对称加密结果", string(date))
date, err = DeRsaPrivate(date, "/Users/tianzhiwei/go/src/webapp/PriveteKey.pem")
if err != nil {
panic(err)
}
fmt.Println("非对称加密解密结果", string(date))
}
/*
生成私钥操作流程
1.使用rsa中GenerateKey方法生成私钥
2.通过x509标准将得到的rsa私钥序列化为ASN.1的DER编码字符串
3.将私钥字符串设置到pem格式块中
4.通过pem将设置好的数据进行编码,并写入磁盘文件中
生成公钥操作流程
1.从得到的私钥对象中将公钥信息取出
2.通过x509标准将得到的rsa公钥序列化为ASN.1的DER编码字符串
3.将公钥字符串设置到pem格式块中
4.通过pem将设置好的数据进行编码,并写入磁盘文件中
*/
func GeneRsa(blockSize int) error {
PrivateKey, err := rsa.GenerateKey(rand.Reader, blockSize)
if err != nil {
return err
}
stream := x509.MarshalPKCS1PrivateKey(PrivateKey)
block := pem.Block{
Type: "RSA PrivateKey",
Bytes: stream,
}
PrivateFile, err := os.Create("PriveteKey.pem")
if err != nil {
return err
}
err = pem.Encode(PrivateFile, &block)
PublicKey := PrivateKey.PublicKey
stream1, err := x509.MarshalPKIXPublicKey(&PublicKey)
if err != nil {
return err
}
block1 := pem.Block{
Type: "RSA PublicKey",
Bytes: stream1,
}
PublicFile, err := os.Create("PublicKey.pem")
if err != nil {
return err
}
err = pem.Encode(PublicFile, &block1)
return err
}
/*
公钥加密
1.将公钥取出得到PEM编码的字符串
2.将得到的字符串进行pem解码
3.使用x509进行解析公钥
4.使用Rsa对公钥进行加密
私钥解密
1.将私钥取出得到PEM编码的字符串
2.将得到的字符串进行pem解码
3.使用x509进行解析私钥
4.对私钥使用rsa进行解密
*/
func EnRsaPublic(filePath string, src []byte) ([]byte, error) {
file, err := os.Open(filePath)
msg := []byte(" ")
if err != nil {
return msg, err
}
//(file *File) Stat() (FileInfo, error)
info, err := file.Stat()
//type FileInfo interface
if err != nil {
return msg, err
}
byteSize := make([]byte, info.Size())
//(f *File) Read(b []byte) (n int, err error) Read方法从f中读取最多len(b)字节数据并写入b
file.Read(byteSize)
//Decode(data []byte) (p *Block, rest []byte)
block, _ := pem.Decode(byteSize)
//type Block struct
//ParsePKIXPublicKey(derBytes []byte) (pub interface{}, err)
pubinter, err := x509.ParsePKIXPublicKey(block.Bytes)
if err != nil {
return msg, err
}
pubKey := pubinter.(*rsa.PublicKey)
//EncryptPKCS1v15(rand io.Reader, pub *PublicKey, msg []byte)
msg, err = rsa.EncryptPKCS1v15(rand.Reader, pubKey, src)
if err != nil {
return msg, err
}
return msg, nil
}
func DeRsaPrivate(src []byte, filePath string) ([]byte, error) {
file, err := os.Open(filePath)
msg := []byte(" ")
if err != nil {
return msg, err
}
//(file *File) Stat() (FileInfo, error)
info, err := file.Stat()
//type FileInfo interface
if err != nil {
return msg, err
}
byteSize := make([]byte, info.Size())
//(f *File) Read(b []byte) (n int, err error) //Read方法从f中读取最多len(b)字节数据并写入b
file.Read(byteSize)
block, _ := pem.Decode(byteSize)
priKey, err := x509.ParsePKCS1PrivateKey(block.Bytes)
if err != nil {
return msg, err
}
msg, err = rsa.DecryptPKCS1v15(rand.Reader, priKey, src)
if err != nil {
return msg, err
}
return msg, nil
}
